1.2 計算論的アプローチと精神医学
1.2.1 計算論的神経科学
計算論的神経科学は、神経系の生物学的構造とメカニズムを情報処理の観点から形式化します。計算論的神経科学は、神経科学、認知科学、心理学、工学、コンピュータ科学、数学、生物物理学などの分野の交差点にある高度に学際的な分野です。過去25年間でこの分野は大きく成長しました。11991年から2016年まで、この分野は年間2本の査読付き科学論文から年間400本以上の出版物へと200倍以上成長しました。1980年代半ば、2つの主要な要因がこの急成長につながりました(Abbott 2008)。
最初の要因は、人工ニューラルネットワークにおけるバックプロパゲーションアルゴリズムの実装と広く採用されたことに関連していました(Rumelhart, Hinton, and Williams 1986; セクション2.1を参照)。バックプロパゲーションの採用は、ニューラルネットワークモデルが処理できるタスクの数を大幅に拡大し、結果として、これらの技術で解決可能な問題に興味を持つ科学者の数も増加しました。
2番目の要因は、物理学からの重要な概念と数学的アプローチを神経科学に翻訳したことに関わっていました(第2章を参照)。例えば、1980年代には、ジョン・ホップフィールドやダニエル・アミットのような物理学者が、無秩序な磁石に関連する理論的問題に対処するために元々開発された統計的手法を用いて、記憶モデルをさらに優雅に分析できることを示しました(Amit, Gutfreund, and Sompolinsky 1985; Hopfield 1982)。
物理学から採用されたような数学モデルは、より抽象的な模式図や言葉による記述よりも明確な利点があります。これらは、モデルを導き出す際に、モデラーに可能な限り正確で、自己一貫性があり、完全であることを強制します。そのようなモデルは、異なる目的のために使用できます。
- 利用可能なデータを簡潔かつ統合的に記述し、可能であれば異なるデータセットを同じ形式で統一する(つまり、「何が?」という問いに答える – 研究対象の現象の基本的な特性は何か?)。
- 観察されたデータを可能な根底にあるメカニズムと関連付ける(つまり、「どのように?」という問いに答える – ある現象に必要な十分な条件はどのようにして現れるのか?)。
- 観察された行動が、理論的に正当化できる原理の結果として「なぜ」現れるのかを理解する(例:ある生物学的、環境的、または発達上の制約下での個々の最適化プロセスを理解することを通じて)。
モデルが答えられる問いを記述する際に、マーの分析レベルに言及することも一般的です(Marr 1982; 図1.4)。マーは、情報処理システムを3つの明確で補完的な分析レベルで理解できると提案しました。
- 計算レベル(Computational Level):一般的な入出力マッピングの観点から、解決すべき問題を特定します(例:「リストのソート」)。
- アルゴリズムレベル(Algorithmic Level):問題がどのように解決され、どのような表現を使用し、その表現を構築および操作するためにどのようなプロセスを用いるかを特定します(例:「クイックソート」、「バブルソート」)。
- 実装レベル(Implementational Level):物理的な部品とその組織のレベルです(例:特定のプログラミング言語)。アルゴリズムを実行する物理的メカニズムを記述します。
これらのレベルはほとんど独立して機能し、多くの場合、異なる数学モデルを使用して記述できます。課題は、これらの記述レベルを橋渡しし、それらがどのように互いに制約し合うかを理解することです。
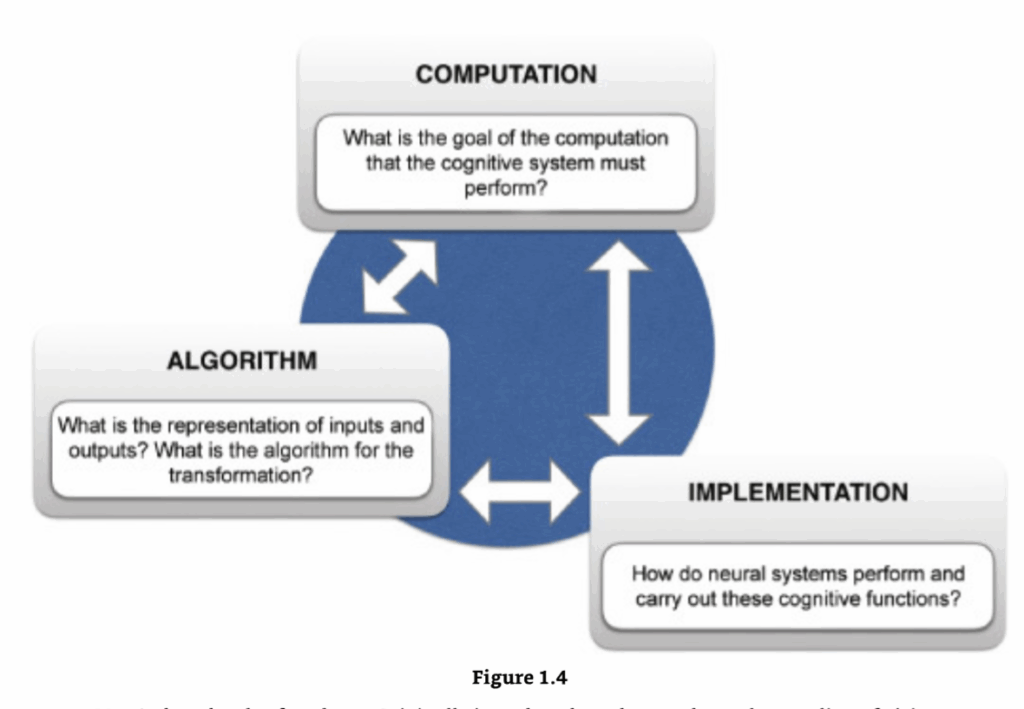
マーの3つの分析レベル
もともと視覚の理解を進めるために導入されたマーのアプローチは、神経科学の文脈における情報処理を考察する3つの明確な方法(計算レベル、アルゴリズムレベル、実装レベル)を提唱しました。この区別は、その後、他の認知ドメイン(例:記憶、注意、学習)における研究にも使用されてきましたが、多くの研究者はマーの階層の古典的な厳密なフレームワークを厳密に採用していません。代わりに、この階層は、分析の異なるレベルにおける明確な概念的問いを強調するための整理原則として最も一般的に使用されています。画像提供:Debbie Yee and Todd Braver。
計算論的アプローチは、基本的な神経生物学的現象の記述方法を劇的に変化させました。成功し影響力のある理論モデルの例としては、神経の電圧と活動の変化の単純なモデルを提供するラピケの統合発火モデル(Lapicque 1907; Lapicque 1926)(セクション2.1.5を参照)、活動電位の生成と伝播におけるナトリウムおよびカリウムチャネルの動態の詳細な記述を提供するホジキン=ハクスリーの活動電位モデル(Hodgkin and Huxley 1952)、神経電圧が神経突起(軸索や樹状突起など)の様々な形態学的特性とどのように関連するかを記述するラルのケーブル理論(Rall et al. 1977)、そしてニューラルネットワーク内の神経接続の強さ(例:学習の結果としてのシナプス可塑性)を更新するためのアルゴリズムを提供するヘブの可塑性規則(Hebb 1949)があります。
神経科学における根本的な理論的進歩は、脳における情報符号化と計算の捉え方も変えました。これは例えば、バーロウの予測コーディング仮説における情報理論の応用を通じて見ることができます(セクション2.4.6も参照)。理論神経科学の著名な人物であるホレス・バーロウ(1985)は、感覚系の階層的組織が2つの必須事項を反映していると示唆しました。(1) 環境における統計的規則性を検出するために、最大限の新しい情報を取り入れること、そして (2) これらの学習された規則性を利用して環境に関する予測を構築することです。これらの予測は、適応行動を導くために使用されます。言い換えれば、彼は脳が、知覚環境の統計情報に最適化された情報処理戦略を用いることによって、感覚情報を効率的に符号化するように進化したと提唱しました(Olshausen and Field 1997)。このフレームワークは、脳が純粋な反応的な感覚器官としてではなく、予測エンジンとして機能し、世界の統計に関する内部モデルを用いて、置かれている環境と取るべき最善の行動を継続的かつ自動的に推論していることを示唆しています。
最近では、認知機能の計算モデルが精神病理学を説明するために使用できると提案されています。例えば、予測コーディングに関与するプロセスの障害は、自閉症における心の理論の欠如から、統合失調症における滑動性追従眼球運動の異常に至るまで、様々な観察結果を説明できる可能性があります(セクション2.4.6と第6章を参照)。このようなアイデアの発展は、「計算精神医学」という分野の誕生を告げました。
1.2.2 計算精神医学
簡単に定義すると、計算精神医学は、計算モデリングと理論的アプローチを精神医学の問いに適用することから構成されます。まだ非常に若い分野ですが、計算精神医学はすでに非常に多様な分野であり、精神医学、心理学、コンピュータ科学、神経科学、電気・化学工学、数学、生物物理学などの概念を活用しています。計算精神医学は、神経系がどのように、そしてなぜ調節不全な方法で情報を処理し、それによって精神病理学的状態と行動の全スペクトルを引き起こすのかを理解しようとしています。精神科の機能不全がどのように機械的に発生し、分類され、予測され、臨床的に対処されるのかを解明しようとしています。計算精神医学モデルは、生物学に基づいた理論と厳密な分析方法を通じて、異なる分析レベルを結びつけるためにも使用できます。
計算モデリングを精神医学に統合することは、いくつかの基本的な方法で研究を支援できます。第一に、形式化された計算モデルでは、臨床的特徴付け、調整因子、実験仮説の根底にあるすべての仮定が明確にされなければなりません。操作された(独立)変数と測定された(従属)変数の両方を、数学的公式の因子として含めることができます。実験結果がモデル予測と一致する程度は、私たちのメカニズム的理解を定性的かつ定量的に知らせ、将来の実験を導きます。このように、計算モデルの開発とテストは、精神病理学の複雑さの理解を深めるための明確な反復的アプローチを提供します。さらに、計算モデルは時間を明示的に組み込むことができ、機能的な神経認知アーキテクチャがどのように発達するかを理解し、異常な発達軌道に関連する重要な時間窓を特定する能力を向上させます。
計算神経科学におけるより広範な役割と同様に、計算モデルは、精神病理学を特徴づける可能性のある神経情報処理の違いに関して、精神科研究者が3つの基本的な質問に答えるのに役立ちます。
- 何が精神病理学に関与する主要な生物学的構成要素であり、これらの構成要素間の数学的関係は何ですか?計算論的アプローチは、認知機能とその障害の基本的な構成要素の明確で正確な定義を必要とします。
- どのようにして個々の生物学的単位の機能不全やそれらの相互作用が、精神疾患に見られる行動の変化につながるのですか?この質問への回答は、精神疾患に関連する感情的、認知的、行動的問題を治療するために、システムの標的を絞った動的な操作を可能にするかもしれません。
- なぜこれらの変化が起こったのですか?動的システムにおける病因の理解は最も困難です。なぜなら、初期の、最初の変化がいくつかのノードに下流効果をもたらした可能性があるからです。したがって、完全な調査には、計算モデルに時間を統合し、様々な神経発達軌道にわたる縦断的デザインを使用してその予測値をテストすることが必要です。
神経科学と精神病理学の間のギャップを埋めようとするこのアプローチは、RDoC研究フレームワークと一致しています。なぜなら、特定の神経回路(何)を参照して精神病理学を概念化し、心理学的構成概念と神経生物学的機能の関係(どのように)を理解しようとし、生物学的および環境的病因の両方が神経発達の軌跡(なぜ)に与える影響を明示的に考慮しているからです。これらの質問に関する進展は、精神疾患への潜在的な予防アプローチの範囲を広げるはずです。
1.2.3 データ駆動型アプローチ
幅広い計算論的アプローチが存在しますが、精神医学における計算モデルは、データ駆動型モデルと理論駆動型アプローチの2つの大きなグループに分けられます(Huys, Maia, and Frank 2016b)。本書では理論駆動型モデルに焦点を当てています。しかし、両アプローチは補完的であり、どちらも有望であり、組み合わせることも可能です。
計算精神医学に対するデータ駆動型アプローチは、現在の心理学的または神経生物学的理論に明示的に言及することなく、精神科患者に関連する膨大なデータに機械学習技術を適用することと記述できます。目標は、分類、治療選択、または治療結果の予測に意味のある、高次元データセット(例:遺伝学、神経画像所見、行動パフォーマンス、自己申告アンケート、治療反応など)間の新しい統計的関係を見つけることです。ここで、前提となるのは、精神疾患の理解が、主にデータ品質、量、分析の改善を通じて向上するというものです。この「盲目的な」または「力ずくの」アプローチは、研究者が、潜在的に時代遅れの歴史的視点ではなく、多面的な臨床データに純粋に基づいて新しい理論を生成することを可能にするかもしれません(Huys et al. 2016b)。
図1.5は、データ駆動型アプローチが、精神疾患の伝統的な症状ベースのカテゴリーを超えた新しい記述と分類にどのように繋がるかを示しています。様々な気分障害(例:大うつ病性障害、気分変調性障害、双極性障害)を持つ患者集団を考えてみましょう。これらの患者に関連する遺伝的、生理学的、脳活動、行動データ、および社会的、文化的、環境的要因の範囲に機械学習技術を適用すると、新しい、偏りのない導き出された生体行動学的クラスターの発見につながる可能性があります。このようなクラスターは、元のDSM分類よりも均質なグループを形成し、疾患の根本原因とより直接的に結びつく可能性があります。
1.2.4 理論駆動型アプローチ
理論駆動型モデルは、本書の焦点であり、「古典的な」計算神経科学のアプローチを精神医学の問いに適用することと記述できます。一般に、これらのモデルは、観察可能な変数(例:行動)と理論的に関連するが、潜在的に観察できない生物学的メカニズムとの間の関係を数学的に記述します。理論駆動型モデルは、脳の解剖学および/または生理学、または基本的な理論が開発されている高次機能(例:知覚、学習、意思決定)の既知の実験的知識を一般的に組み込みます。これらのモデルは、神経生物学的ネットワークの認知/行動機能が既知である場合、および/またはモデルを制約するための正確で詳細な実験データが利用可能である場合に特に有用です。理論駆動型モデルは、分子から複雑な行動まで、複数の分析レベルと抽象化レベルにわたることができます。それらは、既存のデータが回路の測定された生理学的行動を説明するのに十分であるかどうかを示すことができます。また、説明されていない生物学的メカニズムがデータをよりよく説明できるかどうかを強調し、知識のギャップを指摘することもできます。
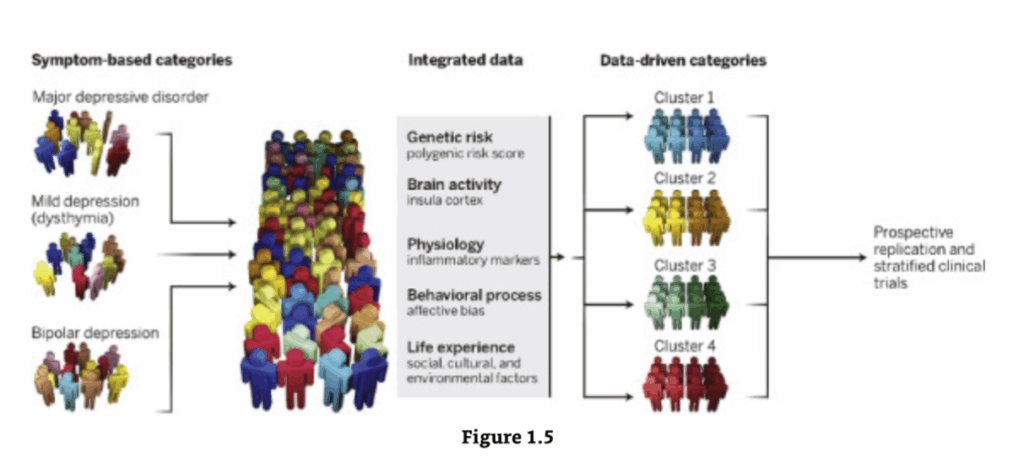
データ駆動型計算精神医学
データ駆動型アプローチが、精神疾患の伝統的な症状ベースのカテゴリーを超えて、新しい記述と分類につながる可能性を示す仮想的な例を以下に示します。様々な種類の気分障害を患い、様々なデータ(遺伝子、脳、生理学的データなど)が収集されている患者集団を考えてみましょう。データの中に、症状の根底にあるメカニズムとより直接的に関連する新しいクラスターが見つかる可能性があります。このようなクラスターは、元の分類よりも均質なグループを形成し、可能な治療の観点からより関連性が高い可能性があります。Insel and Cuthbert (2015) より許可を得て転載。
以下では、理論駆動型モデルの代表的な3つの例について議論します。これらは、生物物理学的に現実的なニューラルネットワークモデル、強化学習モデル、ベイジアンモデルです(Huys et al. 2016b)。
生物物理学モデル
生物物理学モデルは、精神疾患に見られる生物学的異常が神経行動力学にどのように影響するかを解明するためによく使用されます。生物物理学モデルは、単一のニューロンとシナプスの本質的な計算が、ホジキンとハクスリー(1952)によって提案されたタイプの一次微分方程式のセットによって捉えられるという理論的仮定に基づいています。合成計算モデルは、ニューロンの生物物理学的に現実的な特性を再現し、行動コンテキストにおける神経生理学的システムの提案された入出力特性をテストするために使用できます(Wang and Krystal 2014; Ferrante et al. 2016; Huys et al. 2016b; Shay et al. 2016)。生物学モデルは、生物学的知識基盤が十分に確立されており、患者集団における自然な変動を最もよく説明する生物学的メカニズムを特定するのに役立つ場合に最も適しています。生物学的に現実的なモデルは複雑さに幅があり、生物学的詳細の最適な程度は問われる科学的質問に依存します。単純なモデルはより一般化可能ですが、複雑なモデルは生物学的リアリズムを高めるにつれて、その還元主義的な魅力が失われる可能性があります。生物学的リアリズムは計算コストが高いため、これらのモデルは、ネットワークが比較的小さい場合や、関連する生物学的パラメーターが比較的少ない場合に最も容易に実装できます。複雑なシステムの基本的な生物学的特徴を組み込んだ還元主義的アプローチは、生物学的メカニズム、神経計算、および機能出力間の関係を解明するための最も単純な可能なフレームワークとなり得ます。例としては、報酬予測誤差と関連付けられたドーパミン信号のモデル、持続的な神経活動として内部表現されるワーキングメモリ、知覚的意思決定タスクにおける神経積分器などがあり、これらすべては精神医学で観察される一部の認知障害の理解に関連しています(第2〜4章を参照)。一方で、精神病などの他の精神症状を説明するためには、生物学的に現実的なモデルを使用することは時期尚早かもしれません。なぜなら、細胞レベルおよびシステムレベルでの明確な神経生理学的特徴付けがまだ不足しているからです(Wang and Krystal 2014; 第6章も参照)。
強化学習モデル
研究分野としての強化学習は、数理心理学、人工知能、制御理論の交差点に位置しています。これは、人工であろうと自然であろうと、あらゆる種類のシステムが、非常に複雑な環境(迷路内の場所などの状態や、状態間の遷移を含む)において、どのように報酬を獲得し、罰を回避することを学習できるかを探求します。これらは、エージェントが何を最適化しようとしているのかという明確な概念の下で、エージェントがどのように「すべき」行動をとるかを記述します。その意味で、これらは行動を理解するための規範的なフレームワークを提供します。
強化学習は、これまで独立して追求されてきた2つの長く豊かな研究伝統の組み合わせから生まれました(Sutton and Barto 2018)。1つ目の流れは、最適制御と価値関数および動的計画法を用いた解法に関するものです。最適制御は、特定の最適性基準が達成されるように、与えられたシステムに対する制御法則を見つける問題に対処する数学的技術に関連します。2つ目の流れは、試行錯誤による学習に関するものです。この流れは、動物学習の心理学、特にパブロフ(古典的)条件付けと道具的(オペラント)条件付けの科学的探求にその起源を見出します。
- 古典的条件付けとは、中立的な刺激(条件付け刺激と呼ばれる)が、無関係な報酬または罰の刺激(無条件刺激と呼ばれる)と関連付けられ、行動反応(条件付け反応と呼ばれる)を生み出す学習の一形態です。パブロフが研究した有名な例では、ベル(条件付け刺激)と食べ物(無条件刺激)の繰り返しのペアリングにより、ベルだけが提示されたときに犬がよだれを出す(条件付け反応)ようになりました。
- 道具的条件付けは、行動と結果の間の関連付けの学習に関連します。B.F.スキナーは、正の強化に続く行動は繰り返される可能性が高く、負の強化に続く行動は消滅する可能性が高いことを示しました。
パブロフ条件付け、道具的条件付け、およびその後の研究は、動物と人間が環境における物体、行動、および強化の偶発性間の関連付けを自然に学習し、この学習を使用して将来の結果を予測することを示しています。学習はこれらの予測を最適化するために(または予測誤差を減らすために)起こります。興味深いことに、オペラント条件付けの研究は、特に望ましい行動を強化し、望ましくない行動を排除するように設計された方法を提供する一部の現代の心理療法、特に行動心理療法の基礎も形成しています。このように、これらのモデルは精神医学と自然に関連しています。
病変研究、薬理学的操作、行動中の動物における電気生理学的記録、およびヒトにおけるfMRI信号からの収束する証拠は、強化学習モデルと神経構造の間の関連性を提供しています。特に、かなりの量の文献は、神経調節物質であるドーパミンが重要な強化信号、すなわち時間差報酬予測誤差を提供することを示唆しています(セクション2.3および5.3を参照)。ドーパミン依存的な時間差モデルは、神経調節(しばしば精神疾患で調節不全になると仮説が立てられている)、薬剤治療、乱用薬物、および学習システム間の重要なつながりを提供します。
ベイジアンモデル
最後に、現代の計算神経科学における主要なアイデアは、脳が環境を解釈し、私たちの行動を導くために、世界の内部確率モデルを維持し、更新しているというものです。そうすることで、それはよく知られた統計的手法であるベイズ推論に似た計算を使用します(セクション2.4を参照)。ベイズ推論の方法は、より多くの証拠や情報が利用可能になるにつれて、仮説の確率を更新するために使用されます。精神医学に適用される場合、このアプローチは、精神疾患を、脳が歪んだ内部確率モデルを通じて世界を解釈しようとするか、またはそのような内部モデルを感覚情報と誤って組み合わせ、不適応な信念を生成するものとして概念化します。
ベイジアンモデルは、期待される行動を予測し(与えられたタスクで最適な行動は何だろうか)、機能不全な行動の重症度を最適性からの「距離」として定量化し、不適応な信念がどのように生じるかを理解するのに特に役立ちます。伝統的に、ベイズ推論は主に行動データに適用されてきましたが、最近では行動データを神経データやfMRIデータと統合する試みがなされています(Fischer and Peña 2011; Turner et al. 2013)。
これらの主要なタイプの理論駆動型モデル、すなわち生物物理学モデル、強化学習、予測コーディング、およびベイジアンモデルについては、第2章でさらに詳しく説明されます。
データ駆動型と理論駆動型モデルの相互補完性
もちろん、理論駆動型モデルとデータ駆動型モデルは相互に排他的ではありません。理論駆動型モデルは、しばしば実験データに強く基づいており、それによって検証されます。同様に、データを収集および分析する完全に偏りのない方法は存在せず、しばしば理論として定式化できる仮説が組み込まれています。両方のアプローチは補完的です。最終的には、メカニズム的な神経行動学的軌跡の正確な診断分類、予測、説明を提供するために、それらを組み合わせる必要があります。
両方のアプローチの開発を奨励する多くのイニシアチブが作成されています。前述のように、NIMHのRDoCイニシアチブは、精神科研究者が現在の診断カテゴリーを横断する可能性のある機能不全の焦点を絞った側面を研究し、異なる生物学的分析レベル間のメカニズム的説明を結びつけることを奨励しています。米国のBrain Research through Advancing Innovative Neurotechnologies (BRAIN) Initiativeは、多数の細胞から同時に記録し、高い時空間精度で脳活動を刺激できる革新的な神経技術の開発を促進してきました。これらのイニシアチブが一体となって、最先端の計算モデリングにとって肥沃な土壌となる大規模で複雑なマルチモーダルデータセットを生成しています。
計算精神医学は間違いなく台頭しています。計算精神医学という用語を使用した最初の論文は2007年に発表されました(Montague 2007)。続く10年間で、この分野は急速に拡大し、220の出版物といくつかの専門書が出版されました(Parks, Levine, and Long 1998; Sun 2008; Redish and Gordon 2016; Anticevic and Murray 2017; Heinz 2017; Wallace 2017)。そのような問題に興味を持つグループや、サマースクールやワークショップも最近花開いています。しかし、この分野はまだ黎明期にあり、個人レベルで精神病理学を説明できる包括的なモデルはまだ実装される必要があります。私たちは、この本が新しい科学者の集団を鼓舞し、精神疾患の新しい理解と治療の進歩に役立つことを願っています。
1.3 本書の構成
次のセクションでは、理論駆動型計算精神医学の主要な方法を概観します。ニューラルネットワークとコネクショニスト手法、ドリフト拡散モデル、強化学習モデル、予測コーディング、ベイジアンモデル、および行動データへの計算モデルの適合に関連する方法について説明します。
RDoCの精神(図1.3を参照)に則り、続く3つの章では、行動機能の次元に関連するモデルについて説明し、認知システムおよび正と負のバレンスシステムに重点を置いた健全な機能のモデルに焦点を当てます。第3章では、ワーキングメモリと意思決定の生物学的に詳細なモデルについて説明します。第4章では、認知制御のモデルについて説明します。第5章では、強化システムに焦点を当てます。続く章では、統合失調症(第6章)、うつ病(第7章)、不安(第8章)、依存症(第9章)、およびチック障害(トゥレット症候群、第10章)への計算論的アプローチの適用例を示します。第11章では、第5〜10章で取り上げられなかった疾患に関する追加の指摘と、将来の研究のためのいくつかのガイドラインを提供します。
1.4 章の要約
- 精神疾患の負担は、苦しみ、平均余命、経済的コストの点で非常に大きいです。
- 最近数十年間、新しい薬理学的薬物と治療法の発見は停滞しています。
- 精神疾患の定義と診断は、何世紀にもわたって問題でした。ほとんどの疾患において、単一の原因、単一の有機基質、または単一の時間経過を特定することは不可能である可能性が高いです。DSMとして知られている精神疾患の現在のカテゴリー分類は、臨床的に非常に価値があることが証明されていますが、DSMに基づく診断に関連する異質な表現型と、マニュアルの非理論的な構造は、より効果的な治療につながる可能性のある生物学的メカニズムを考慮することを困難にしています。
- 新しいアプローチは、精神疾患を症状の集まりとして記述することから、神経科学と認知モデリングを精神病理学と橋渡しする方法へと移行することを目指しています。NIMHのRDoCイニシアチブはこのアプローチを奨励しており、計算モデリングはRDoCによって強調されたいくつかの課題(例:異なる分析単位を因果的に関連付けること、時間的軌跡をモデル化すること、神経発達全体における特定の構成要素間の動的相互作用)を解決するための有用なアプローチを提供することができます。
- 計算論的アプローチは、神経科学の進歩の中心であると考えられています。それらは精神医学の分野にも同様に恩恵をもたらす可能性があります。
1.5 さらなる学習
精神医学の分野の歴史的視点については、Fischer (2012) を参照してください。計算精神医学という新たな分野を記述するレビューについては、Montague et al. (2012); Friston et al. (2014); およびStephan and Mathys (2014) を参照してください。NIMHのRDoCイニシアチブについて読むには、Kozak and Cuthbert (2016) を参照できます。

