運動神経科学の計算原理

2000年 Nature America Inc. http://neurosci.nature.com
レビュー

運動神経科学の計算原理
ダニエル・M・ウォルパート¹、ズービン・ガフラマーニ²
¹ ユニバーシティ・カレッジ・ロンドン、神経学研究所、クイーン・スクエア、ソベル神経生理学部、ロンドン WCIN 3BG、英国
² ユニバーシティ・カレッジ・ロンドン、クイーン・スクエア、ギャツビー計算神経科学ユニット、ロンドン WCIN 3AR、英国
連絡先：D.M.W. (wolpert@hera.ucl.ac.uk)
運動の統一原理が運動制御の計算論的研究から明らかになった。我々はこれらの原理のいくつかをレビューし、運動計画、制御、推定、予測、学習などのプロセスにそれらがどのように適用されるかを示す。我々の目標は、計算論的アプローチから生じる特定のモデルが、運動神経科学の理論的枠組みをどのように提供するかを示すことである。

運動制御の計算論的研究は、基本的に感覚信号と運動指令の関係に関係している。運動指令からその感覚的結果への変換は、環境の物理学、筋骨格系、感覚受容器によって支配される。感覚信号から運動指令への変換は、中枢神経系（CNS）内のプロセスによって決定される。私たちの行動の複雑さの多くは、これら2つの変換の単純な結合として生じる。

CNSは運動から感覚への変換を表現する必要はないが、これは物理世界によって実装されているため、CNSがこの変換を内部的に表現しているという認識から、エキサイティングな計算的および実験的発展が生まれている。この変換の側面をモデル化するシステムは、行動とその結果との間の因果関係をモデル化するため、「順方向内部モデル」として知られている。これらのモデルの主な役割は身体と世界の行動を予測することであるため、「予測子」と「順方向モデル」という用語を同義的に使用する。所望の結果から行動への逆の変換を実装するシステムは、「逆方向内部モデル」として知られている。我々は「内部モデル」という用語を使用して、CNSが感覚運動系をモデル化していること、そしてこれらがCNSのモデルではないことを強調する。

ベルマン¹は、このような変換を表現する際に、必要なストレージと計算数が感覚および運動アレイの次元とともに指数関数的に増加することを指摘し、この問題を「次元の呪い」と呼んだ。これは、人間の体にある600ほどの筋肉が、極端な単純化のために、収縮しているか弛緩しているかのいずれかであると考えると鮮明に示される。これにより、2⁶⁰⁰もの可能な運動活性化が生じ、これは宇宙の原子の数よりも多い。これは明らかに、運動活性化から感覚フィードバックへの単純なルックアップテーブル、およびその逆を禁止する。幸いなことに、制御にとって、完全なセンサーおよびモーターアレイよりもはるかに低い次元を持つコンパクトな表現、すなわちシステムの「状態」として知られるものを一般に抽出することができる。システムの固定パラメータと物理学を支配する方程式とを合わせると、状態には、システムの未来を予測または制御するために必要なすべての関連する時間変動情報が含まれる。たとえば、投げられたボールの現在の位置、速度、スピン、つまりボールの状態を知ることで、ボールのすべての原子の構成を知る必要なく、その将来の経路を予測できる。

一般に、状態、例えば筋肉群（シナジー）の活性化のセットや手の位置と速度は、運動中に急速かつ連続的に変化する。しかし、操作される対象の同一性や、より遅い時間スケールでの四肢の質量など、他の重要なパラメータは離散的に変化する。我々は、そのような離散的またはゆっくりと変化するパラメータを運動の「文脈」と呼ぶ。正確で適切な運動行動を生成する我々の能力は、運動指令を一般的な運動文脈に合わせることに依存している。

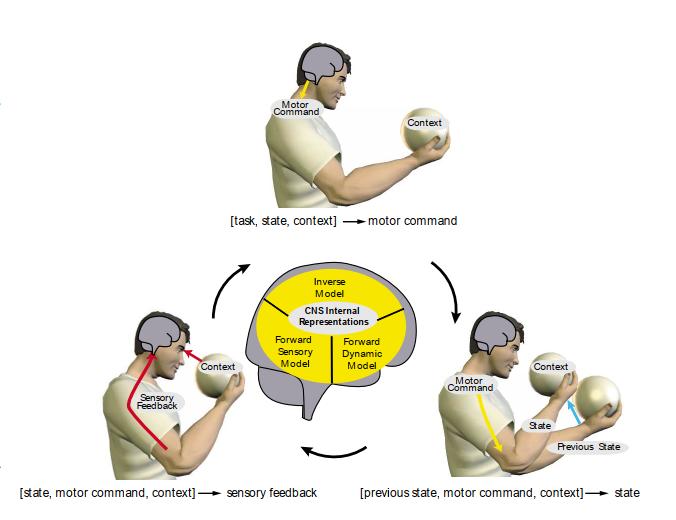
感覚運動ループ（図1）は、感覚運動系の全体的な行動を支配する3つの段階に分けることができる。第1段階では、状態と特定のタスク（図1、上）が与えられたときにCNSによって生成される運動指令を指定する。第2段階では、運動指令（図1、右）が与えられたときに状態がどのように変化するかを決定する。第3段階では、この新しい状態（図1、左）が与えられた感覚フィードバックを指定することによってループを閉じる。これら3つの段階は、逆モデル、順動力学モデル、順感覚モデルとして、CNS内で内部モデルとして表現される。

我々は、計画、制御、学習などの計算論的運動制御のすべての主要なテーマが、タスクがどのように行動を決定するか、運動指令がどのように生成されるか、状態と文脈がどのように推定および予測されるか、そして内部モデルがどのように表現および学習されるかを考慮することから生じることを示す。仮想現実技術と新しいロボットインターフェースの出現により、初めて、洗練されたコンピュータ制御環境を作成することが可能になった。被験者が相互作用する世界の物理学をこのように制御できるようになったことで、計画、制御、学習の計算モデルの詳細なテストが可能になった（例、文献2-6）。

タスク：運動計画

日常生活のタスクは、一般に、グラスから水を飲むなど、高次の、しばしば象徴的なレベルで指定される。しかし、運動系は最終的に、関節の回転や宇宙空間での手の軌道につながる筋肉の活性化を指定するという、詳細なレベルで機能しなければならない。高レベルのタスクと低レベルの制御の間には明らかにギャップがある。実際、ほとんどすべてのタスクは、原理的には無限の異なる方法で達成することができる。たとえば、唇に水の入ったグラスを持ってくる方法は、賢明なものから馬鹿げたものまで、数多くある。これらすべての可能性を考えると、ほとんどすべての研究がどのようにして、

図1. 感覚運動ループ。運動指令の生成（上）、状態遷移（右）、感覚フィードバックの生成（左）を示す。中央は、CNS内のこれらの段階の内部表現を示す。

モーターコマンド
コンテクスト
[タスク、状態、コンテクスト]
逆モデル
CNS内部表現
モーターコマンド
順方向
感覚
モデル
順方向
動的
モデル
コンテクスト
モーターコマンド
感覚
フィードバック
モーターシステムが特定のタスクを解決する方法は、タスクの繰り返しと、同じタスクに取り組む個人との間で、非常に定型化された運動パターンを示すことを示しています。ニューヨークからロンドンまでのさまざまなルートをランク付けできるのと同じように、タスクに対する可能な運動を評価するための基準があれば、CNSは最善のものを選択できます。最適制御は、まさにそのような選択問題を扱うためのエレガントなフレームワークであり、したがって、高レベルのタスクから詳細な運動プログラムに変換できます。具体的には、コストが運動とタスクの何らかの関数として指定され、最もコストの低い運動が実行されます。課題は、コスト関数、つまり、観察された運動パターンと摂動研究から、何が最適化されているかをリバースエンジニアリングすることです。
[状態、運動指令、コンテクスト] 感覚フィードバック
運動の最適制御モデルは、手の軌道とトルク指令の滑らかさを最大化することに基づいて提案されています。これらのモデルは、経験データの範囲をうまく再現しますが、なぜ滑らかさが重要なのか、そしてそれがCNSによってどのように測定されるのかは不明です。さらに、これらのモデルは、腕のような単一の運動システムに限定されています。最近、目と腕の目標指向運動のための統一コストを提供するモデルが提案されています。このモデルは、運動指令にノイズがあり、ノイズの量が運動指令の大きさに比例すると仮定しています。そのようなノイズが存在する場合、意図された運動指令の同じシーケンスを何度も繰り返すと、運動の確率分布が生じます。この分布の側面、例えば、運動の終了時の手の位置や速度の広がりなどは、運動指令のシーケンスを変更することによって制御できます。このモデルでは、タスクは分布の側面がどのようにペナルティを課されるかを指定し、これがコストを形成します。たとえば、単純な照準運動では、タスクは、ターゲットに関する分散によって測定される最終誤差を最小限に抑えることです。図2は、2つの可能な運動指令のシーケンスの結果を示しています。1つは、もう1つよりも高いエンドポイントのばらつき（青い楕円体）につながります。最適制御戦略の目的は、楕円体の体積を最小限に抑え、それによって可能な限り正確にすることです。このモデルは、サッカード眼球運動と腕の運動の両方の軌道を正確に予測します。滑らかでない運動は大きな運動指令を必要とし、それによってノイズが増加します。滑らかさはしたがって正確さにつながりますが、それ自体が目標ではありません。コスト、つまり運動誤差は、行動的に関連性があり、CNSが測定するのに簡単です。小脳への訓練信号として機能する可能性のあるクライミングファイバーは、運動の終了時のそのような到達誤差をコードします¹⁰。コスト関数は最適な運動を指定しますが、新しい、練習されていない運動に対してこの最適にどのようにアプローチするかは未解決の問題です。

運動指令：制御

運動指令がどのように生成されるかについて、いくつかのモデルが提案されています。最初の提案の1つは、CNSが
状態
前の状態
[前の状態、運動指令、コンテクスト] → 状態
空間パラメータを指定し、筋肉と反射ループのばねのような特性に依存して手足を動かす¹¹⁻¹³。たとえば、このモデルの一形態では、一連の筋肉活性化が空間における手の安定した平衡位置を定義します。運動は、所望の軌道に沿ったそのような平衡位置の連続によって達成されます¹⁴。このモデルは、筋肉と脊髄の特性をフィードバックコントローラーとして使用して、所望の軌道に沿って手を引きます。システムのダイナミクスにより、筋肉と反射ループの剛性（平衡からの単位変位あたりに生成される力）が高くない限り、実際の位置は所望の軌道を正確に追従しません。代替案として、逆モデルを構築して、軌道に沿った各点での所望の状態を運動指令にマッピングするという提案があります¹⁵。これら2つのアプローチは、ボールを円形の経路に沿って動かすという問題を、それに作用する力を指定することによって対比することができます。逆モデル制御では、運動方程式は
運動A
位置
分布
運動B

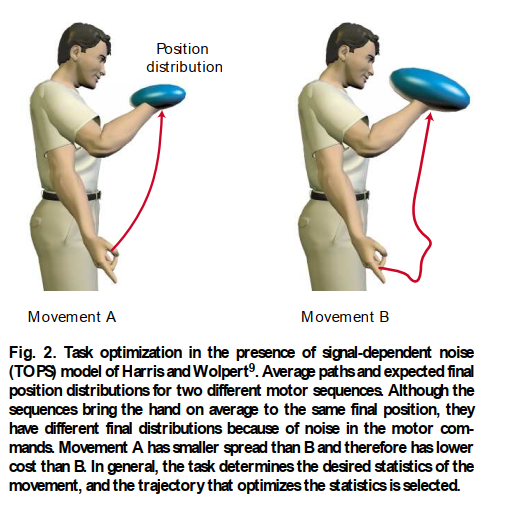
図2. 信号依存ノイズ（TOPS）が存在する場合のタスク最適化。HarrisとWolpertのモデル。2つの異なる運動シーケンスの平均経路と期待される最終位置分布。シーケンスは平均して同じ最終位置に手をもたらすが、運動指令のノイズのために最終分布が異なる。運動AはBよりも広がりが小さいため、Bよりもコストが低い。一般に、タスクは運動の所望の統計を決定し、統計を最適化する軌道が選択される。

前の状態
推定
ダイナミクス
予測子
モーター
コマンド
Eferenceコピー
予測された
現在の状態
+
+
現在の状態
推定
感覚ベース
補正
感覚
予測子
予測された感覚
フィードバック
+
カルマン
ゲイン
感覚
フィードバック
感覚
フィードバック
モーター
コマンド

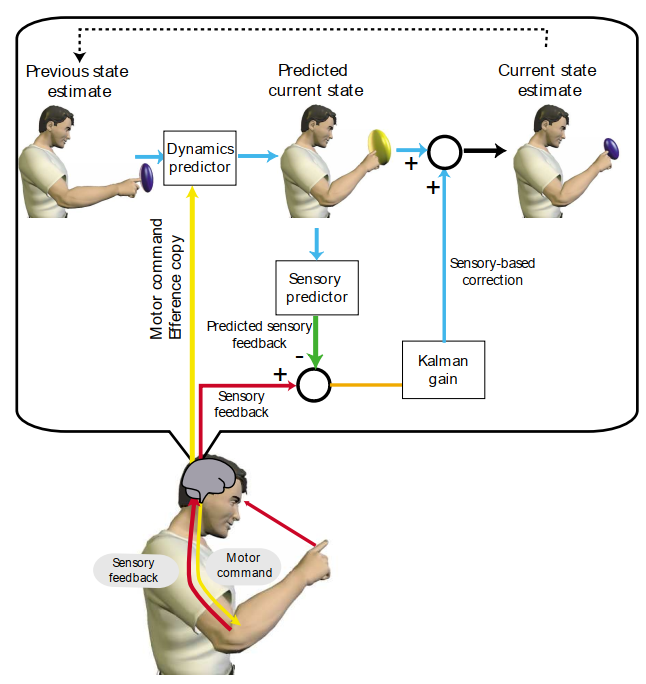
図3. カルマンフィルターモデルが運動中の指の位置を再帰的に推定する一ステップの概略図。現在の状態は、可能な指の位置の分布を表す前の状態推定（左上）から構築され、不確実性の雲（青）として示される。モーターコマンドのコピー、つまりエフェレンスコピーと、ダイナミクスのモデルにより、この前の状態から現在の状態分布を予測できる。一般に、不確実性は増加する（黄色の雲）。この新しい推定は、現在の感覚フィードバックを予測するために使用されることでさらに洗練される。この予測と実際の感覚フィードバックとの間の誤差は、現在の推定を修正するために使用される。カルマンゲインは、この感覚誤差を状態誤差に変換し、エフェレンスコピーと感覚フィードバックに置かれる相対的な信頼性も決定する。最終的な状態推定（右上）は、不確実性が減少している（青い雲）。感覚信号、赤矢印；モーターコマンド、黄色矢印；状態信号、青矢印。感覚フィードバックの遅延は補償されなければならないが、明確にするために図から省略されている。

望ましい加速度を生成するためにボールに適用される力と解かれます。平衡点制御の場合、ボールは制御点にばねで取り付けられており、制御点は単に円形の経路に沿って移動し、ボールはそれに沿って追従します。ボールが円に沿って移動するためには、ばねの剛性、つまり筋肉と反射ループを表すものが高くなければなりません。剛性が低い場合、たとえばスリンキーが使用された場合、制御された点とボールの経路は非常に異なります。対照的に、逆モデルを使用すると、腕は低い剛性で制御できます。現在、運動中の腕の剛性によって測定されるゲインについては議論があり、ある研究では剛性が低いことが示唆されています。低い剛性では、平衡点制御では観察される単純な運動を達成するために複雑な平衡軌道が必要となり、したがって計算的に魅力的な解決策ではなくなります。

運動指令の最終的な共通経路は、約20万個のα運動ニューロンによって形成されます。この運動出力のコーディングが何であり、高レベルの目的が運動指令でどのように表現されるかという疑問が生じます。脊髄では、実験は、いくつかの運動プリミティブまたは基底関数¹⁶を活性化することによって制御が達成されるという、計算上魅力的な考えを支持しています。この考えは、各筋肉を個別に制御するのではなく、筋肉活性化のパターンなどの少数のプリミティブを異なる割合で組み合わせることによって制御を単純化することです。そのような制御は、運動出力の有効次元を減少させます。カエルの脊髄刺激研究は、脊髄が外部空間の力場に対応するプリミティブを介して運動を制御し、複雑な運動¹⁷、¹⁸を構築するための「文法」を提供するために組み合わせることができることを示唆しています。各力場プリミティブは、異なる形状の谷と考えることができます。水が景観の最も低い点まで何らかの経路に沿って流れ落ちるのと同じように、腕は力場の中で平衡点まで移動します。谷を合計することによって、新しい景観、つまり行動を構築できます。

高レベルでは、運動皮質では、個々のニューロンと集団¹⁹⁻²³内で何がコードされているかについてかなりの議論がありました。提案には、運動の方向、速度、加速度、姿勢、関節トルクが含まれます。最近のモデル²⁴は、皮質が筋肉群を活性化し、これらの相反する見解の多くは、皮質活動、筋肉フィルタリング特性、運動キネマティクス間の関係を考慮することで解決できることを提案しています。観察された運動のキネマティクスを考えると、モデルは、運動皮質ニューロンが上記の運動特性のすべてをエンコードすることが期待されることを示しています。

状態：推定と予測

感覚運動ループの3つの段階のいずれかをモデル化するには（図1）、CNSは現在の状態を知る必要がありますが、2つの問題に直面します。第一に、感覚信号のCNSへの変換と輸送にはかなりの遅延が伴います。第二に、CNSは、ノイズによって汚染されている可能性があり、状態に関する部分的な情報しか提供しない可能性のある感覚信号からシステムの状態を推定する必要があります。たとえば、私たちが打ったばかりのテニスボールを考えてみましょう。単にボールの網膜上の位置を使用してその位置を推定した場合、私たちの推定は約100ミリ秒遅れます。より良い推定は、順方向モデルを使用してボールが実際にどこにあるかを予測することによって行うことができます。第二に、ボールのスピンは直接観察できませんが、ボールの見えた経路、つまり時間とともに統合された感覚情報を使用して推定できます。この推定は、ボールがどのように打たれたか、つまりボールのダイナミクスの内部順方向モデルと組み合わせて運動指令を知ることで改善できます。感覚フィードバックと順方向モデルを使用して現在の状態を推定するこの組み合わせは、「オブザーバー」として知られており、その例がカルマンフィルター²⁵です（図3）。オブザーバーの主な目的は、感覚運動の遅延を補償し、感覚と

運動信号。線形システムの場合、カルマンフィルターは、二乗誤差が最も少ない状態で状態を推定するという点で最適な観測者である。このようなモデルは、手の位置3,26、姿勢27、頭の向き28の推定を調べる経験的研究によって裏付けられている。頭頂葉皮質の損傷は、そのような状態推定を維持できなくなる可能性がある29。
観測者の枠組みを使用すると、現在の状態を推定することから、将来の状態と感覚フィードバックを予測することまで、単純な計算ステップである。このような予測には多くの潜在的な利点がある30。状態予測は、感覚フィードバックが利用可能になる前に行動の結果を推定することにより、感覚運動ループにおけるフィードバック遅延の影響を軽減することができる。このようなシステムは、熟練した操作の根底にあると考えられている。たとえば、手に持った物体が加速されると、指は物体の滑りを防ぐために予測して握りを強める。これは予測に依存するプロセスである（レビューについては、文献31を参照）。状態予測は、意図された運動の精神的シミュレーションにも使用できる。頭頂葉皮質の損傷は、影響を受けた手で運動を精神的にシミュレートできなくなる可能性がある32。
感覚予測は、状態予測から導出でき、運動の感覚的効果、つまり再帰性を相殺するために使用できる。このようなシステムを使用することにより、自己運動によって誘発される感覚変化の効果を相殺し、それによってより関連性の高い感覚情報を強化することが可能である。このようなメカニズムは、電気魚で広範囲に研究されており、そこでは小脳のような構造に依存している（たとえば、文献33）。霊長類では、神経生理学的研究34は、頭頂葉皮質における予測的更新を示しており、眼球運動の網膜上の結果を予測している。人間では、予測的メカニズムは、くすぐりのような同じ触覚刺激が自己適用されると、より弱く感じられるという観察の根底にあると考えられている。自己適用された触覚刺激の強度の低下は、運動35の予測された感覚的結果と実際の感覚的結果との間の正確な時空間的整合性に決定的に依存する。同様に、感覚予測は、運動が自己生成されたものであるか、したがって予測可能であるか、または外部で生成されたものであるかを決定するメカニズムを提供する。このメカニズムの失敗は、患者に自分の体が自分以外の力によって動かされているように見えるという制御の妄想の根底にあると提案されている36。興味深いことに、左頭頂葉皮質の損傷は、見られる運動が自分のものであるかそうでないかを判断する相対的な能力の低下につながる可能性がある37。

文脈：推定

異なる物理的特性を持つオブジェクトと相互作用すると、私たちの運動の文脈は離散的な形で変化します。

プリアー
コンテキスト1
(空)
コンテキスト2
(フル)
0.2
0.8
ミルク
プリアー
予測子
コンテキスト1 予測された
(空) フィードバック
尤度 (小さい
予測誤差)
= 0.99
文脈の確率
(事後確率)
0.89
エフェレンス
コピー
コンテキスト2
(フル)
感覚
フィードバック
感覚
フィードバック
モーター
コマンド
尤度 (大きい
予測誤差)
= 0.03
ベイズの
法則
0.11

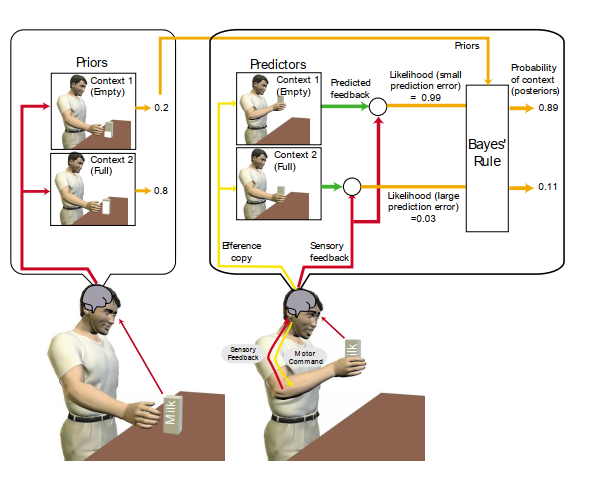
図4. 文脈推定の概略図。2つの文脈、牛乳パックが空か満杯か。最初に、視覚からの感覚情報が2つの可能な文脈の事前確率を設定するために使用され、この場合、パックは満杯である可能性が高いように見える。満杯のパックに適した運動指令が生成されると、運動指令のエフェレンスコピーが2つの可能な文脈の下で感覚的結果をシミュレートするために使用される。空のパックに基づく予測は、満杯のパックの文脈と比較して大きな動きを示唆する。これらの予測は実際のフィードバックと比較される。パックは実際には空であるため、感覚フィードバックは空のパックの文脈の予測と一致する。これにより、空のパックの尤度が高くなり、満杯のパックの尤度が低くなる。尤度は、ベイズの定理を使用して事前確率と組み合わされ、各文脈の最終的な（事後）確率を生成する。

運動系が状態を推定することが不可欠であるのと同様に、変化する文脈も推定しなければなりません。強力な形式主義の1つはベイズ的アプローチであり、これを使用して各文脈の確率を推定できます。確率は2つの項、尤度と事前確率に分解できます。特定の文脈の尤度は、その文脈が与えられた場合の現在の感覚フィードバックの確率です。この尤度を推定するために、その文脈の感覚順方向モデルを使用して、運動からの感覚フィードバックを予測します。予測された感覚フィードバックと実際の感覚フィードバックとの間の不一致は、尤度に反比例します。予測誤差が小さいほど、文脈の可能性が高くなります。これらの計算は、複数の予測モデルが並行して動作するモジュール式の神経アーキテクチャによって実行できます38。それぞれが1つの文脈に調整され、その文脈の相対的な尤度を推定します。したがって、このモデルのアレイは、一連の仮説検証器として機能します。事前確率には、文脈が時間とともにどのように変化するか、また運動前に文脈がどれほどありそうかという構造化された情報が含まれています。尤度と事前確率は、ベイズの定理を使用して最適に組み合わせることができ、これら2つの確率の積をとり、考えられるすべての文脈で正規化して、各文脈の確率を生成します。図4は、実際には空である満杯の牛乳パックのように見えるものを拾う例を示しています。予測モデルは、当初は空のカートンよりも満杯のカートンのコントローラーの出力を重み付けした誤った事前確率をオンラインで修正します。ベイズの定理は、初期戦略が間違っていても、適切な制御への迅速な修正を可能にします。この例には、2つの文脈を表す2つのモジュールがあります。ただし、モジュール式のアーキテクチャは、原理的には、数千のモジュール、つまり文脈に拡張できます。状態と文脈の推定に別々のアーキテクチャが提案されていますが（図3と4）、どちらも不確実な環境でベイズ推論をオンラインで行う方法と考えることができます。
文脈推定に必要なプロセスのこの解釈は、霊長類における最近の神経生理学的研究と一致しており、CNSが特定の文脈³⁹の期待される感覚フィードバックをモデル化し、文脈⁴⁰が与えられた感覚フィードバックの尤度を表すことを示しています。文脈推定の洗練された例として、被験者が胴体を回転させながら到達運動を行うと、胴体から生じる速度依存のコリオリ力に対して補償します。

所望の状態
推定された状態
逆モデル
運動
誤差
フィードフォワード
運動
コマンド
+
+
+
状態
誤差
フィードバック
コントローラー
感覚
フィードバック
運動
コマンド
フィードバック
運動
コマンド

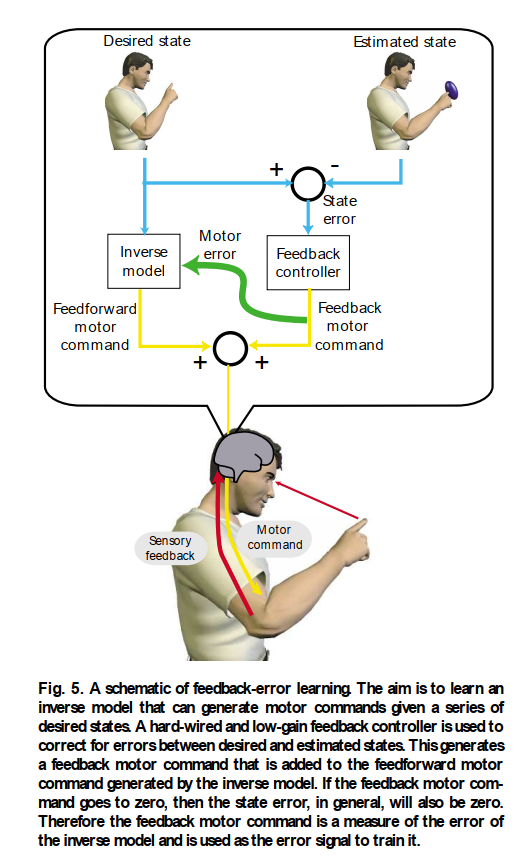
図5. フィードバック誤差学習の概略図。目的は、一連の所望の状態が与えられた場合に運動指令を生成できる逆モデルを学習することである。ハードワイヤードで低ゲインのフィードバックコントローラーが、所望の状態と推定された状態との間の誤差を修正するために使用される。これにより、逆モデルによって生成されたフィードフォワード運動指令に追加されるフィードバック運動指令が生成される。フィードバック運動指令がゼロになると、一般に状態誤差もゼロになる。したがって、フィードバック運動指令は逆モデルの誤差の尺度であり、それを訓練するための誤差信号として使用される。
回転し、腕に作用する。被験者が大きな動く視覚画像によって誘発される錯覚的な自己回転を経験すると、視覚的な事前情報に基づいて、コリオリ力の文脈を期待するように運動を行う。これにより、到達誤差が生じ、その後の運動で、期待されるコリオリ力の感覚的結果が経験されないため、減少する。

内部モデル：学習

順方向と逆方向の両方の内部モデルは、感覚運動系の特性に関する情報を捉えます。これらの特性は静的ではなく、環境との相互作用による短期間の変化と、成長による長期間の変化の両方で、生涯を通じて変化します。したがって、内部モデルは感覚運動系の特性の変化に適応可能でなければなりません。環境は、感覚フィードバックの予測子を学習するための適切なトレーニング信号を容易に提供します。予測された感覚フィードバックと実際の感覚フィードバックの差は、予測モデルを更新するための誤差信号として使用できます。電気魚の小脳様構造におけるそのような予測学習につながる神経メカニズムは、部分的に理解されています³³。
運動学習を通じて逆内部モデルを取得することは、一般的に難しい作業です。これは、適切なトレーニング信号、つまり運動指令誤差が直接利用できないためです。私たちがグーグリーをボウリングするのに失敗したとき、このクリケットの偉業を達成するために筋肉の活性化をどのように変えるべきか誰も教えてくれません。代わりに、私たちは感覚座標で誤差信号を受け取り、これらの感覚誤差は、逆モデルをトレーニングするために使用される前に運動誤差に変換される必要があります。フィードバック誤差学習モデル¹⁵、⁴¹は、この問題に対する巧妙な解決策を提供します（図5）。ハードワイヤードですが、完全ではないフィードバックコントローラーは、所望の状態と推定された状態との間の不一致に基づいて運動指令を計算します。運動指令は、フィードバックコントローラーの運動指令と適応逆モデルの出力の合計です。このモデルの背後にある論理は、フィードバックコントローラーが最終的に運動指令を生成しなくなれば、所望の状態と推定された状態との間に不一致がない、つまりパフォーマンスに誤差がなく、逆モデルが完全に機能しているということです。したがって、フィードバックコントローラーの出力は誤差信号と見なされ、逆モデルをトレーニングするために使用できます。これは非常に成功したアプローチです。神経生理学的証拠⁴²は、この学習メカニズムを、眼球追従応答と呼ばれる単純な反射眼球運動について小脳内で支持しており、小脳が眼のダイナミクスの逆モデルを構築することを示唆しています。
動的学習に関する最近の研究は、逆モデルの表現に焦点を当てています。被験者が、手²に取り付けられたロボットまたは回転室⁴³によって生成された力場でポイントツーポイント運動を行う場合、時間とともに適応し、力場の存在下で自然に動くことができます。このプロトコルを使用して、いくつかの理論的な問題が解決されました。ダイナミクスの学習は関節ベースの座標で一般化され²、学習は経験した状態に依存しますが、その時間的順序⁴⁴には依存せず、状態依存の場は時間的に変化する場⁴⁵よりも効率的に学習され、順方向モデルと逆方向モデルの両方が学習⁴⁶中に同時に適応されます。
単一の文脈の学習を調べることから、さまざまな文脈を学習する方法を検討することに焦点が移り始めています。複数の文脈で行動することを学習できるアーキテクチャの1つは、制御のためのモジュラー選択と識別（MOSAIC）モデルであり、複数の予測子-コントローラーペア³⁸を含んでいます。上記のように、予測子は各文脈の確率を提供し、これらの確率は、各文脈に合わせて調整された対応するコントローラーのセットの出力を重み付けするために使用されます。このシステムは、複数の予測子とコントローラーを同時に学習し、特定の文脈に適したコントローラーを選択する方法を学習できます。
運動学習のメカニズムに関する我々の理解は、ある文脈を学ぶことが他の文脈を学ぶことをどのように妨げるかを調べることから得られました。被験者が2つの異なるダイナミクス⁴⁷、⁴⁸または視覚運動の再配置⁴⁹を学習しようとすると、それらが素早く連続して提示されると干渉が起こりますが、数時間離れている場合は起こりません。これは、運動学習が固化の期間を経ることを示唆しており、その間、運動記憶は破壊されやすいです。興味深いことに、視覚運動と動的摂動は干渉せず、個別に⁴⁹学習できるのと同じくらい速く一緒に学習できます。
私たちが遭遇する多くの状況は、操作されたオブジェクトや環境の新しい組み合わせなど、以前に経験した文脈の組み合わせから派生しています。個々のコントローラーの出力への寄与を変調することにより、最終的な運動指令に、膨大なレパートリーの行動を生成することができます。したがって、複数の内部モデルは、概念的には、膨大な語彙を持つ複雑な運動行動を構築するために使用される構成要素である運動プリミティブと見なすことができます。2つの異なる文脈を学習した後、CNSは、視覚運動ドメイン内と、視覚運動ドメインと動的ドメインの両方で出力を適切に混合できます⁵⁰。

統一原理

計算論的アプローチは、運動制御のための統一原理を提供し始めています。いくつかの共通のテーマがすでに明らかになっています。第一に、内部モデルは、状態推定、予測、文脈推定、制御、学習などのさまざまなプロセスを理解するための基本です。第二に、最適性は、運動計画、制御、推定に関する多くの理論の根底にあり、幅広い実験結果を説明できます。第三に、運動システムは、世界の不確実性とその感覚入力と運動指令のノイズに対処する必要があり、ベイズ的アプローチはそのような不確実性に直面した最適推定のための強力なフレームワークを提供します。これらの、そして他の統一原理が、目、腕、スピーチ、姿勢、バランス、運動などの多様な運動システムの制御の根底にあることがわかると信じています。

謝辞

ピエール・バラデュック、ロバート・ファン・ビアーズ、ジェームズ・イングラム、ケルビン・ジョーンズ、フィリップ・ヴェッターには、原稿へのコメントをいただきました。この研究は、ウェルカムトラスト、ギャツビー慈善財団、ヒューマンフロンティア科学機構からの助成金によって支援されました。

2000年6月16日受理、2000年9月29日採択

Bellman, R. Dynamic Programming (Princeton Univ. Press, Princeton, New Jersey, 1957).
Shadmehr, R. & Mussa-Ivaldi, F. Adaptive representation of dynamics during learning of a motor task. J. Neurosci. 14, 3208-3224 (1994).
Wolpert, D. M., Ghahramani, Z. & Jordan, M. I. An internal model for sensorimotor integration. Science 269, 1880-1882 (1995).
Ghahramani, Z. & Wolpert, D. M. Modular decomposition in visuomotor learning. Nature 386, 392-395 (1997).
Gomi, H. & Kawato, M. Equilibrium-point control hypothesis examined by measured arm stiffness during multijoint movement. Science 272, 117-120 (1996).
Cohn, J. V., DiZio, P. & Lackner, J. R. Reaching during virtual rotation: context specific compensations for expected coriolis forces. J. Neurophysiol. 83, 3230-3240 (2000).
Flash, T. & Hogan, N. The co-ordination of arm movements: An experimentally confirmed mathematical model. J. Neurosci. 5, 1688-1703 (1985).
Uno, Y., Kawato, M. & Suzuki, R. Formation and control of optimal trajectories in human multijoint arm movements: Minimum torque-change model. Biol. Cybern. 61, 89-101 (1989).
Harris, C. M. & Wolpert, D. M. Signal-dependent noise determines motor planning. Nature 394, 780-784 (1998).
Kitazawa, S., Kimura, T. & Yin, P. Cerebellar complex spikes encode both destinations and errors in arm movements. Nature 392, 494-497 (1998).
Feldman, A. G. Functional tuning of the nervous system with control of movement or maintenance of a steady posture. III. Mechanographic analysis of execution by arm of the simplest motor tasks. Biophysics 11, 766-775 (1966).
Bizzi, E., Accornerro, N., Chapple, B. & Hogan, N. Posture control and trajectory formation during arm movement. J. Neurosci. 4, 2738-2744 (1984).
Hogan, N. An organizing principle for a class of voluntary movements. J. Neurosci. 4, 2745-2754 (1984).
Flash, T. The control of hand equilibrium trajectories in multi-joint arm movements. Biol. Cybern. 57, 257-274 (1987).
Kawato, M., Furawaka, K. & Suzuki, R. A hierarchical neural network model for the control and learning of voluntary movements. Biol. Cybern. 56, 1-17 (1987).
Giszter, S. F., Mussa-Ivaldi, F. A. & Bizzi, E. Convergent force fields organized
カエルの脊髄で。J. Neurosci. 13, 467-491 (1993)。
Tresch, M. C., Saltiel, P. & Bizzi, E. The construction of movement by the spinal cord. Nat. Neurosci. 2, 162-167 (1999).
Mussa-Ivaldi, F. A. Modular features of motor control and learning. Curr. Opin. Neurobiol. 9, 713-717 (1999).
Mussa-Ivaldi, F. A. Do neurons in the motor cortex encode movement direction? An alternative hypothesis. Neurosci. Lett. 91, 106-111 (1988).
Sanger, T. Theoretical considerations for the analysis of population coding in motor cortex. Neural Comput. 6, 29-37 (1994).
Georgopoulos, A. P. Current issues in directional motor control. Trends Neurosci. 18, 506-510 (1995).
Scott, S. & Kalaska, J. F. Motor cortical activity is altered by changes in arm posture for identical hand trajectories. J. Neurophysiol. 73, 2563-2567 (1995).
Kakei, S., Hoffman, D. S. & Strick, P. L. Muscle and movement representations in the primary motor cortex. Science 285, 2136-2139 (1999).
Todorov, E. Direct cortical control of muscle activation in voluntary arm movements: a model. Nat. Neurosci. 3, 391-398 (2000).
Goodwin, G. C. & Sin, K. S. Adaptive Filtering Prediction and Control (Prentice-Hall, Englewood Cliffs, New Jersey, 1984).
van Beers, R. J., Sittig, A. C. & van der Gon, J. J. D. Integration of proprioceptive and visual position-information: An experimentally supported model. J. Neurophysiol. 81, 1355-1364 (1999).
Kuo, A. D. An optimal-control model for analyzing human postural balance. IEEE Trans. Biomed. Eng. 42, 87-101 (1995).
Merfeld, D. M., Zupan, L. & Peterka, R. J. Humans use internal model to estimate gravity and linear acceleration. Nature 398, 615-618 (1999).
Wolpert, D. M., Goodbody, S. J. & Husain, M. Maintaining internal representations: the role of the superior parietal lobe. Nat. Neurosci. 1, 529-533 (1998).
Miall, R. C. & Wolpert, D. M. Forward models for physiological motor control. Neural Networks 9, 1265-1279 (1996).
Johansson, R. S. & Cole, K. J. Sensory-motor coordination during grasping and manipulative actions. Curr. Opin. Neurobiol. 2, 815-823 (1992).
Sirigu, A. et al. The mental representation of hand movements after parietal cortex damage. Science 273, 1564-1568 (1996).
Bell, C. C., Han, V. Z., Sugawara, Y. & Grant, K. Synaptic plasticity in a cerebellum-like structure depends on temporal order. Nature 387, 278-281 (1997).
Duhamel, J. R., Colby, C. L. & Goldberg, M. E. The updating of the representation of visual space in parietal cortex by intended eye movements. Science 255, 90-92 (1992).
Blakemore, S. J., Frith, C. D. & Wolpert, D. M. Perceptual modulation of self-produced stimuli: The role of spatio-temporal prediction. J. Cogn. Neurosci. 11, 551-559 (1999).
Frith, C. D. The Cognitive Neuropsychology of Schizophrenia (Lawrenece Erlbaum, Hove, UK, 1992).
Sirigu, A., Daprati, E., Pradatdiehl, P., Franck, N. & Jeannerod, M. Perception of self-generated movement following left parietal lesion. Brain 122, 1867-1874 (1999).
Wolpert, D. M. & Kawato, M. Multiple paired forward and inverse models for motor control. Neural Networks 11, 1317-1329 (1998).
Eskandar, E. N. & Assad, J. A. Dissociation of visual, motor and predictive signals in parietal cortex during visual guidance. Nat. Neurosci. 2, 88-93 (1999).
Kim, J. & Shadlen, M. N. Neural correlates of a decision in the dorsolateral prefrontal cortex of the macaque. Nat. Neurosci. 2, 176-185 (1999).
Kawato, M. & Gomi, H. The cerebellum and VOR/OKR learning models. Trends Neurosci. 15, 445-453 (1992).
Shidara, M., Kawano, K., Gomi, H. & Kawato, M. Inverse-dynamics encoding of eye movement by Purkinje cells in the cerebellum. Nature 365, 50-52 (1993).
Lackner, J. R. & DiZio, P. Rapid adaptation to Coriolis force perturbations of arm trajectory. J. Neurophysiol. 72, 299–313 (1994).
Conditt, M. A., Gandolfo, F. & Mussa-Ivaldi, F. A. The motor system does not learn dynamics of the arm by rote memorization of past experience. J. Neurophysiol. 78, 554-560 (1997).
Conditt, M. A. & Mussa-Ivaldi, F. A. Central representation of time during motor learning. Proc. Natl. Acad. Sci. USA 96, 11625-11630 (1999).
Bhushan, N. & Shadmehr, R. Computational nature of human adaptive control during learning of reaching movements in force fields. Biol. Cybern. 81, 39-60 (1999).
Brashers-Krug, T., Shadmehr, R. & Bizzi, E. Consolidation in human motor memory. Nature 382, 252-255 (1996).
Gandolfo, F., Mussa-Ivaldi, F. A. & Bizzi, E. Motor learning by field approximation. Proc. Natl. Acad. Sci. USA 93, 3843-3846 (1996).
Krakauer, J. W., Ghilardi, M. F. & Ghez, C. Independent learning of internal models for kinematic and dynamic control of reaching. Nat. Neurosci. 2, 1026-1031 (1999).
Flanagan, J. R. et al. Composition and decomposition of internal models in motor learning under altered kinematic and dynamic environments. J. Neurosci. 19, B1-B5 (1999).