2 計算精神医学の方法:概要
Peggy Seriès
エディンバラ大学
「長い人生で学んだことが一つある。それは、私たちの科学はすべて、現実と比べれば未熟で幼稚であるということ。しかし、それが私たちにとって最も貴重なものであるということだ。」
—アルベルト・アインシュタイン、『創造者と反逆者』、1972年
現在、計算精神医学で使用されている方法は非常に多様であり、計算神経科学と認知科学の進歩を反映しており、初期のコネクショニズムから強化学習、確率的手法、応用機械学習まで多岐にわたります。本章では、これらの方法の概要と、さらなる学習のための追加リソースへのヒントを提供します。
2.1 ニューラルネットワークと回路アプローチ
精神的な計算と障害を説明することを目的とした最も初期のモデルは、「コネクショニストモデル」として知られています。ドナルド・ヘブは、1940年代に「コネクショニズム」という用語を導入し、単純なユニット(図2.1)の相互接続されたネットワーク、別名「ニューラルネットワーク」における創発的なプロセスとして精神的または行動的な現象をモデル化する一連のアプローチを記述しました。
これらの単純なユニットは、脳との類推からしばしば「ニューロン」と呼ばれ、その値または「出力」によって記述されます。これはバイナリ(1/0)または実数値でありえます。各ユニットの値は、その入力の合計を「活性化関数」と呼ばれる非線形関数に通したものに等しくなります。ネットワーク接続には通常、「重み」があり、ユニットが互いにどの程度強く影響し合うかを決定します。重みは正または負でありえ、学習手順に従って変化する場合があります。ユニットはまた、閾値を持つ場合があり、受け取った信号の合計がその閾値を超えた場合にのみユニットが活性化されます。
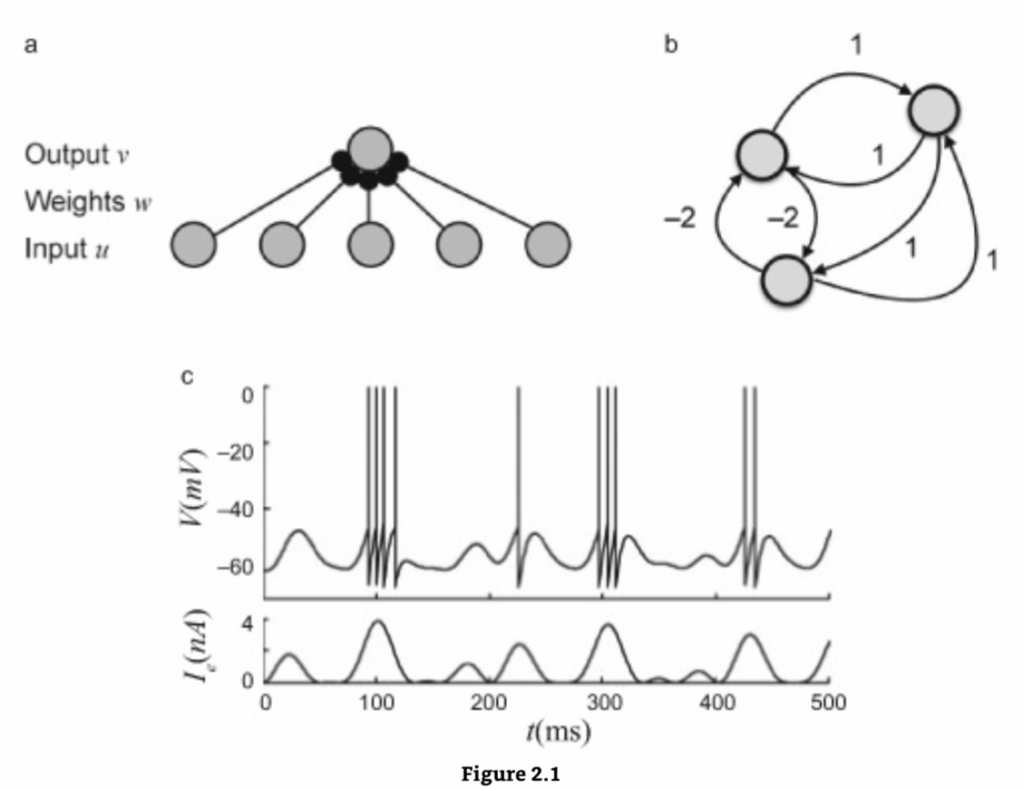
ニューラルネットワークモデルの例
(a) パーセプトロンは順方向ニューラルネットワークです。ここでは、出力ユニット vi が、すべての入力ユニット vj から、重み wij で重み付けされた入力を受け取ります。(b) ホップフィールドネットワークは、再帰的な接続によって接続されたバイナリユニットのネットワークです。(c) 発火統合ニューロン。このモデルは、ニューロンが入力電流 I を受け取ったときに観察される電圧の変化を説明します。電圧が閾値を超えると、電圧は突然0に跳ね上がり、リセットされます。これはスパイク、すなわち活動電位をモデル化しています。
例えば、マカロックとピッツ(1943)は、人工ニューロンの計算モデルとしてバイナリ閾値ユニットを提案しました。このニューロンは、n個の入力信号 xj の重み付き合計を計算します。
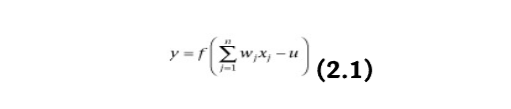
ここで、f はユニットステップ関数として選択され、その値は負の引数に対してはゼロ、正の引数に対しては1となり、合計が特定の閾値 u を超えると1の出力 y を生成します。そうでない場合は0を出力します。wj は j 番目の入力に関連付けられたシナプスの重みです。正の重みは興奮性シナプスに対応し、負の重みは抑制性シナプスをモデル化します。マカロックとピッツは、原則として、このモデルがAND、OR、XORゲート(後者はAND、NOT、ORユニットを組み合わせることで)などのあらゆるブール論理関数を実装できることを証明しました。これらの論理ゲートは、現代のデジタルコンピュータが構築されているデジタル論理電子回路の構成要素です。したがって、原則として、そのような回路はあらゆる種類の計算を達成できます。マカロックとピッツのニューロンは多くの方法で一般化されてきました。ユニットステップ関数の代わりに異なる種類の活性化関数を使用できます。例えば、シグモイド関数、例えばロジスティック関数:f(x)=1/(1+exp(−bx))(ここで b は傾きパラメータ)などです。
2.1.1 人工ニューラルネットワークのアーキテクチャ
人工ニューラルネットワークは通常、層状に構成されています。ニューラルネットワークは**順方向(フィードフォワード)型と再帰型(リカレント)**型に分けられます。
順方向ネットワークでは、情報は一方向のみに流れます。入力ノードから、中間ノード(存在する場合、これらは「隠れ」ノードとも呼ばれます)を通り、最終的に出力ノードへと進みます。たとえば、多層パーセプトロンは、ニューロンが層に組織され、それらの間に単方向の接続を持っています。ネットワーク内にはサイクルやループは存在しません。
一方、再帰型ネットワークでは、同じ層のユニット間も相互に接続されています。順方向ネットワークが、与えられた入力から1セットの出力値しか生成しないという点で静的または「記憶を持たない」のに対し、再帰型ネットワークは値のシーケンスや豊かな時間的ダイナミクスを生成できます。脳内のニューロンもループを持つ回路で密接に相互接続されており、振動のような豊かなダイナミクスを生成できるため、再帰型ネットワークはより生物学的に妥当であると考えられています。
2.1.2 順方向ネットワークにおける学習
ニューラルネットワークにおける学習は、特定のタスクを効率的に実行できるようネットワークのアーキテクチャと接続の重みを更新する問題と見なされます。このタスクは、与えられた入力に望ましい出力をマッピングすることとして定義されます。理論的なレベルでは、主に3つの学習パラダイムを区別できます。
- 教師あり学習(Supervised learning):ネットワークには、訓練データセットのすべての入力パターンに対して正しい出力が与えられます。既知の正しい出力に可能な限り近い答えをネットワークが生成できるように、重みが動的に更新されます。これは、誤差修正則と呼ばれる学習規則を用いて達成されます。
- 強化学習(Reinforcement learning):教師あり学習の一種ですが、ネットワークには出力の正しさに関する評価(正しい/間違っている、または報酬/罰)のみが与えられ、正しい答えそのものは提供されません。
- 教師なし学習(Unsupervised learning):訓練データセットの各入力パターンに関連する正しい答えを必要としません。データの根底にある構造やパターン間の相関関係を探求し、これらの相関関係からパターンをカテゴリに組織化します。
誤差修正則の基本的な原理は、ネットワークの実際の出力と望ましい出力(Ydesired−Yactual)との間の誤差を用いて、勾配降下法として知られる方法により、この誤差を徐々に減少させるように接続の重みを修正することです。
例えば、パーセプトロン学習則はこの誤差修正原理に基づいています。パーセプトロンは、調整可能な重み wj と閾値 u を持つ接続を介して、複数の入力 x=(x1,x2,…,xn) を受け取る単一のニューロンで構成されます(図2.1a)。ニューロンの正味入力 v は以下のようになります。
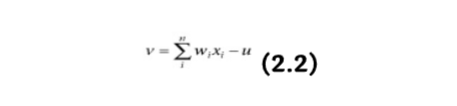
そして、出力は v>0 であれば+1、そうでなければ0に設定されます。パーセプトロンは、入力の2つのクラスを分類するために使用できます。ある一連の入力は1の出力につながるように訓練され、別の入力は0の出力につながるように訓練されます。ローゼンブラット(1958)は、これを以下の手順で達成できることを示しました。
- 重みと閾値を小さな乱数で初期化します。
- パターン j に対して入力ベクトル xj={xj1,xj2,…,xjn} を提示し、ニューロンの出力 yj を評価します。
- 以下の式に従って重みを更新します。
wi(t+1)=wi(t)+η(dj−yj(t))xji (2.3)
そして、dj はパターン j に対する望ましい出力、t は反復回数、η は学習率であり、試行ごとに重みを損失勾配(損失関数の勾配)に対してどれだけ調整するかを決定します(η が低いほど、勾配の下降勾配に沿って移動する速度が遅くなります)。
他のほとんどの**人工知能(AI)**研究者と同様に、ローゼンブラットはニューラルネットワークの力について非常に楽観的で、「パーセプトロンは最終的に学習し、意思決定を行い、言語を翻訳できるようになるかもしれない」と熱心に予測しました。しかし、ミンキーとパパート(1969)は、一般的な結果として、単層パーセプトロンはできることが非常に限られていることを示しました。つまり、線形分離可能なパターンしか分離できないのです。例えば、XOR関数を実装することには失敗しました。これはニューラルネットワークで達成できることに関して壊滅的な結果と認識され、1970年代から1980年代にかけて「AIの冬」として知られる時期、すなわち人工知能研究への資金提供と関心が減少した時期の一因となりました。
AIの冬は1980年代半ばに終わりを告げました。ジョン・ホップフィールドとデビッド・ルーメルハートの研究がニューラルネットワークへの関心を再燃させたのです。ルーメルハート、ヒントン、ウィリアムズ(1986)は、誤差修正則を多層ネットワークに適応させることができ、バックプロパゲーションアルゴリズムという、ニューラルネットワークがあらゆる非線形関数を近似できる方法を提供しました。このようなネットワーク(およびそれに続く派生形)は、文字認識や音声認識などの高度な分類や最適化タスクを実行するように訓練できます。これらの新しい結果は、この分野の新たな成長につながりました。ニューラルネットワークは1990年代に商業的に成功を収めることになります。当初は初期のコンピュータの計算能力によって制限されていましたが、この研究は、同様の原理に基づいた現在の深層学習ネットワークの成功への道を開きました。
2.1.3 再帰型ネットワークとアトラクターダイナミクス
バックプロパゲーションアルゴリズムが導入されたのとほぼ同時期に、物理学者のジョン・ホップフィールドは、ホップフィールドネットと呼ばれる別の形式のニューラルネットワークが、まったく新しい方法で情報を学習および処理できることを証明しました。ホップフィールドネットのユニットは、パーセプトロンと同様にバイナリ閾値ユニットであるため、ユニットの合計入力が閾値を超えるかどうかに応じて、通常+1と−1の2つの異なる値のみを取ります(図2.1b)。ホップフィールドネットの接続には通常、以下の制約があります。i) どのユニットもそれ自体との接続を持たない: wii=0; ii) 接続は対称である: wij=wji。
ホップフィールドネットワーク内の1つのユニットの更新は、以下の規則を用いて行われます。
xi(t+1)=Sgn(∑j=iwijxj(t)+bi) (2.4)
ここで、Sgn(x) は出力が+1または−1である符号関数、wij はユニット j からユニット i への接続の重み、xj はユニット j の状態、bi はユニット i の閾値です。
ホップフィールドネットワークでの更新は、2つの異なる方法で行うことができます。非同期更新では、一度に1つのユニットのみが更新されます。このユニットはランダムに選択することも、事前に定義された順序を最初から課すこともできます。同期更新では、すべてのユニットが同時に更新されます。これは、同期を維持するためにシステムに中央クロックを必要とします。
重要なことに、ホップフィールドは、ネットワークがエネルギー E(スピングラスのポテンシャルエネルギーとの類推による)と呼ばれる量によって記述できることを発見しました。これは以下のように定義されます。
E=−21∑i=jwijxixj−∑ibixi (2.5)
ネットワークの状態がネットワークのダイナミクスに従って進化すると、E は常に減少し、最終的にアトラクターと呼ばれる局所的な最小点に到達し、そこでエネルギーは一定に保たれます。ホップフィールドはまた、これらのエネルギー最小値が特定のn次元パターン(e1,e2,…,ep)に対応するように設定できることを示しました。これは、ユニット j からユニット i への重みを、各パターンの i 番目と j 番目の要素の平均積(すべてのパターンにわたる)に対応するように設定することによって行われます。
wij=p1∑k=1peikejk (2.6)
ek=(e1k,e2k,…,enk) は符号化されるパターン番号 k を示します。これは記憶段階と呼ばれます。その後、ネットワークは連想記憶として使用できます。いわゆる検索段階では、ネットワークに初期状態として使用される入力が与えられ、ネットワークはそのダイナミクスに従って進化し、最終的に入力に最も類似する記憶されたパターンに対応する平衡状態に到達します。例えば、5つのユニットを持つホップフィールドネットを訓練して、状態 (1,−1,1,−1,1) がエネルギー最小値となるようにし、ネットワークに状態 (1,−1,−1,−1,1) を与えると、それは (1,−1,1,−1,1) に収束します。
2.1.4 精神医学への応用
バックプロパゲーションアルゴリズムとホップフィールドネットワークの発見は、ニューラルネットワークへの強い関心再燃を引き起こしました。認知科学において、ニューラルネットワークの観点から知的能力を説明しようとする運動としてのコネクショニズムは、1986年の**並列分散処理(PDP)**の登場によってさらに刺激を受けました。これは、心理学者ジェームズ・L・マクレランドとPDPグループによって編集された2巻の論文集(Rumelhart, McClelland, and PDP Group 1987)で、特に大きな影響を与えました。コネクショニズムは、認知、知識、学習、そしてそれらの障害について新しい理論を提示しました。理論的には、ニューラルネットワークは、人間レベルの参加者と同じくらい高度なタスク(パターン分類、カテゴリ化、関数近似、予測、最適化、コンテンツアドレス可能メモリ、制御)を実行するように訓練することができます。PDPアプローチは、例えば精神疾患で観察されるような認知機能の障害が、根底にあるニューラルネットワークの構造または要素の障害(例:一部の接続の破壊、一部のユニットのノイズの増加)によって説明できるという考えにつながりました。
例えば、コネクショニストモデルは統合失調症に顕著に適用されてきました。統合失調症や躁病の患者は、幻覚や妄想、および会話における急速に変化する、緩慢な連想を特徴的に示すことがあります。初期の研究では、ホップフィールドネットワークのダイナミクスを支配するパラメータがこれをどのように再現するかを調査しました。ノイズの増加は、記憶の特異性を低下させ、統合失調症における連想の広がりを反映し、不安定で常に変化する記憶につながる可能性があります。同様に、過剰な刈り込みを模倣する接続の削除、または容量を超える記憶によるネットワークの過負荷は、幻覚や妄想を思わせる局所的な寄生的なアトラクターの出現を引き起こします(レビューについては、Hoffman and McGlashan 2001を参照)。
2.1.5 生物学的ネットワーク
より最近では、そのような仮説は、より生物学的に現実的なニューラルネットワークの文脈で探求されています。これらのネットワークは、実際のニューロンについて知られていることを模倣する、いわゆる「スパイク発火ニューロン」で構成されています。生物学的ニューロンは、活動電位または「スパイク」として知られる、電圧の短く突然の増加を使用して情報を送信します(図2.1c)。**リーキー発火統合ニューロン(LIF)**は、スパイク発火ニューロンモデルの最も単純な例かもしれませんが、その分析とシミュレーションの容易さから依然として非常に人気があります。
ニューロンの時刻 t における状態は、そのソマの膜電位 v(t) によって記述されます。ニューロンは、入力 I(t) の「リーキーインテグレータ」としてモデル化されます。
τdtdv(t)=−v(t)+RI(t) (2.7)
ここで、τ は膜時定数、R は膜抵抗です。電子工学の用語では、この方程式は単純な抵抗-コンデンサ(RC)回路を記述しています。ニューロンの膜は、電荷を蓄積し分離する能力があるため、コンデンサとして記述できます。イオンチャネルは電流が細胞内外に流れることを可能にします。より多くのイオンチャネルが開いている場合、より多くのイオンが流れることができます。これは抵抗の減少を表し、コンダクタンスの増加につながります。
スパイクのダイナミクスはLIFモデルでは明示的にモデル化されていません。代わりに、膜電位 v(t) が特定の閾値 vT(スパイク閾値)に達すると、瞬時に低い値 vreset(リセット電位)にリセットされ、方程式(2.7)で記述されたリーキー積分プロセスは初期値 vreset で新たに開始されます。より現実性を加えるために、v(t) が閾値 vT を超えた直後に絶対不応期 Δabs を追加することが可能です。絶対不応期の間、v(t) は vreset にクランプされ、スパイク後 Δabs の遅延後にリーキー積分プロセスが再開されます。
入力電流は定数であることも、動的であることもあります。ニューロンがネットワークの一部としてモデル化されている場合、入力電流は他のニューロンから来るシナプス入力を反映します。これらは、各接続に重み(興奮性ニューロンの場合は正、抑制性ニューロンの場合は負)が与えられる重み付けされた入力として、または実際のシナプス入力(興奮性シナプス後電位、別名EPSP、および抑制性シナプス後電位、別名IPSP)のダイナミクスをモデル化するシナプスコンダクタンスとして、より現実的な方法でモデル化することができます。
個々のニューロンと生物学的に現実的なニューロンのネットワークのモデリングに関するより詳細な情報は、例えば Dayan and Abbott (2000) で見つけることができます。
第3章では、このようなスパイク発火ニューラルネットワークを、健常者および統合失調症患者における意思決定とワーキングメモリの欠陥を理解するために適用する方法について説明します。統合失調症患者は、優勢な反応の抑制を必要とする認知柔軟性と制御タスクにも障害を示します。第4章では、これらのタスクに関与する回路をモデル化することが、精神疾患における認知制御の欠陥のより良い理解につながる方法を示します。
2.2 ドリフト拡散モデル²
ドリフト拡散モデル(DDM) (Ratcliff 1978) は、物理学に触発された別のクラスのモデルに属します。ここでは、根底にある可能性のある生物学的基質を気にすることなく、動物や人間が2つの選択肢の間で単純な意思決定を行う際のパフォーマンスという、特定の心理的プロセスの現象論的記述を提供することを目的としています。これらのモデルは興味深いものです。なぜなら、当初は心理学的プロセスの現象論的記述としてのみ提案されていましたが、現在では、最適な意思決定理論の概念や実際の生物学的ニューロンで観察される動的プロセスとも関連していることが明らかだからです。
DDMは、比較的速い意思決定(通常2秒未満)に適用され、単一段階の意思決定プロセスにのみ適用されます(例えば、推論タスクに関与する可能性のある多段階プロセスとは対照的)。このようなタスクには、例えば知覚的弁別(これら2つの物体は同じか異なるか?)、認識記憶(この画像は新しいものか、以前に提示されたものか?)、語彙判断(これは単語か非単語か?)などがあります。パフォーマンスは反応時間と正確さの観点から記述されます。このようなタスクは、精神医学で、異なるグループにおける情報処理方法を評価するためによく使用されます。例えば、不安やうつ病の参加者が、単純な意思決定をしなければならないときに、脅威的または否定的な情報を対照群と異なる方法で処理するかどうかを判断するためです。
ドリフト拡散モデルは、意思決定に関与する異なる要素、特に、意思決定に入る証拠の質を意思決定基準や、刺激符号化や反応実行などの非意思決定プロセスから分離することを目指しています。これらのモデルでは、意思決定は、閾値に達するまでノイズのある証拠を蓄積することによって行われ、その時点で反応が開始されます(図2.2)。
DDMにはいくつかの数学的表現が存在します。典型的な方程式はウィーナー過程(1次元ブラウン運動)の形式をとります。拡散過程 x(t) は動的に以下のように進化します。
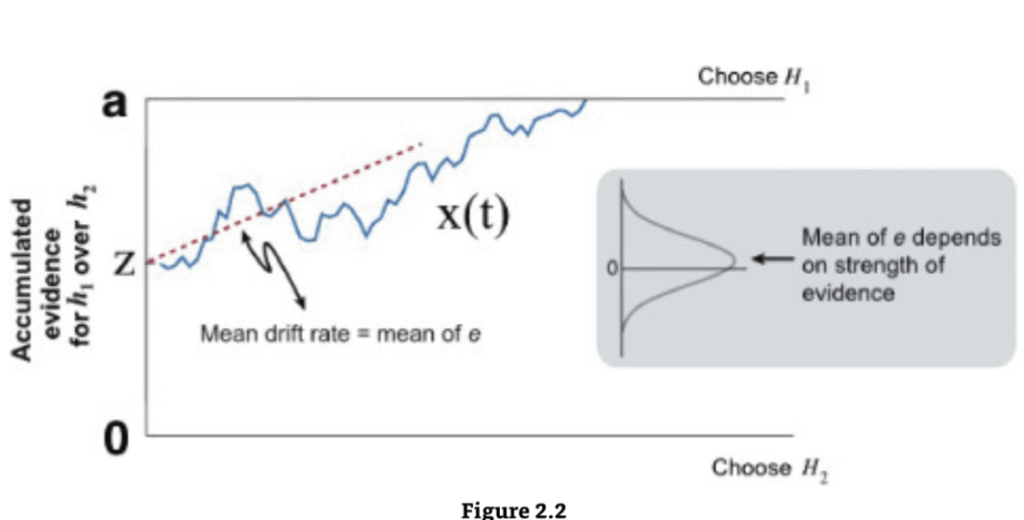
ドリフト拡散モデル(DDM)
意思決定変数は、出発点 [0,a] の中央にある(出発点に偏りがない)証拠 (e) から構成されるノイズのある累積プロセス(青)です。証拠は、その平均 μ が証拠の強さに依存するガウス分布からサンプリングされます。境界は停止規則を表し、その分離は正確性-速度のトレードオフを説明します。Gold and Shadlen (2007) より許可を得て転載。
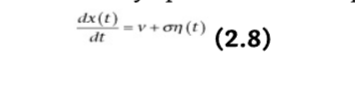
- ドリフト率 v:刺激からの情報証拠の質を表します。刺激が容易に分類できる場合、ドリフト率は高くなり、正しい境界に素早く接近するため、迅速で正確な反応につながります。
- η(t):ホワイトノイズ項です。
- σ2:プロセスの分散です。
モデルでは、ノイズのある証拠が開始点 z から2つの境界のいずれか、すなわち a または 0 に到達するまで蓄積されます。2つの境界は、はい/いいえ、単語/非単語などの2つの可能な意思決定を表します。プロセス x(t) が境界に達すると、対応する応答が開始されます。
モデルの各構成要素、すなわち境界分離 (a)、ドリフト率 (v)、開始点 (z)、および非意思決定処理 (T) には、直接的な心理学的解釈があります。
- 開始点 z の位置は、反応バイアスを示します。個人がある反応に偏っている場合(例:各選択肢の頻度が異なる、または報酬が異なる)、その開始点は対応する境界に近くなります。これは、その反応を行うためにより少ない証拠しか必要としないことを意味します。これにより、他の境界と比較して、その境界でより迅速かつ高確率な反応が起こります。
- 2つの境界の分離 a は、反応の注意深さまたは速度/正確性の設定を示します。広い境界分離は慎重な反応スタイルを反映します。この場合、累積プロセスが境界に到達するまでにより時間がかかりますが、誤って間違った境界に到達する可能性が低くなり、遅いですが正確な反応が生成されます。
開始点、ドリフト率、非意思決定時間の試行間変動を捉えるパラメーターを追加することもできます。このような変動は、モデルが正しい反応と誤反応の相対的な速度を正確に説明するために必要です。また、モデルを拡張して、拡散意思決定プロセス以外の何らかのプロセス(例:注意の途絶)から生じる応答、すなわち**汚染物(contaminants)**を含めることで、異常な応答やデータ中の外れ値を説明することも可能です。
このモデルは、経験的なRT分布の特性である右偏りを生成するため、選択プロセスの満足な記述であることが示されました。拡散モデルのより数学的な詳細については、興味のある読者は Ratcliff and Tuerlinckx (2002) または Smith and Ratcliff (2004) を参照できます。
DDMには、RTおよび/または正確性の従来の分析よりもいくつかの利点があります。まず、行動データを処理コンポーネントに分解できます。これにより、研究者は反応の注意深さ、反応バイアス、非意思決定時間、刺激証拠の値を比較できます。このアプローチにより、研究者は被験者グループ間の違いの源をよりよく特定できます。
例えば、White et al. (2010b) は拡散モデルを用いて、高不安な個人の脅威情報処理がどのように異なるかを研究しました。彼らの語彙判断実験では、参加者に文字の列が示され、それが単語であるか非単語であるかを判断しなければなりませんでした。一部の単語は脅威的な単語であり、他の単語は中立的でした。彼らは、異なる入力間の競合がない状況でも、高不安な個人において脅威的な単語に対する一貫した処理上の利点を発見しました。一方、従来の比較では有意な差は示されませんでした。具体的には、高不安な参加者は、非脅威的な単語と比較して脅威的な単語に対するドリフト率が大きく、低不安な参加者はそうではありませんでした。
このモデルのもう1つの利点は、RTと正確性を同時にフィッティングすることで、識別することが非常に困難な異なる種類のバイアスを特定するのに役立つことです。特に、弁別性(刺激からの証拠の質の変化)と反応バイアス(意思決定基準のシフト)を区別することができます。最後に、古典的な分析がRTや正答率を個別に調べるのとは異なり、すべてのデータを一度に使用するため、違いを検出する感度が高い可能性があります。
2.2.1 最適性とモデルの拡張
DDMの多くの拡張とバリアントが提案されています。一方で最適性理論、他方で意思決定の神経学的研究との関連により、時間の経過とともに意思決定境界が崩壊するモデルが生まれました。このモデルでは、時間が経過するにつれて意思決定をトリガーするために必要な証拠が少なくなります。同様の効果を持つ別のバリアントは、固定された境界を持ちますが、蓄積された証拠に「緊急信号」が追加されます。
最近の研究では、DDMを強化学習モデルと統合することで、学習効果を説明できることが示されています(Pedersen, Frank, and Biele 2017)。このようなモデルでは、強化学習スキームを用いて各選択肢の報酬期待値が計算され、動的に更新されます。一方、DDMは選択メカニズムであり、ドリフト率は2つの選択肢の報酬期待値の差に依存します。
また、DDMのランダムウォークは、証拠が時間とともに蓄積されるときに統計的に最適な意思決定を行う手順である逐次確率比検定(Bogacz et al. 2006)と容易に関連づけられることが長年知られています。DDMとベイジアンモデルとの厳密な数学的等価性は、最近明示的に導出されました(Bitzer et al. 2014)。2つ以上の選択肢間のより長く、より複雑な意思決定を説明するために、他の拡張も提案されています(Roe, Busemeyer, and Townsend 2001)。
臨床疾患と個人差の調査に適用されたDDMモデルのレビューについては、White et al. (2010b) および White, Curl, and Sloane (2016) を参照してください。
2.2.2 生物学的ニューロンにおける証拠の蓄積
脳が拡散型アルゴリズムを使用しているかどうかは、非常に興味深く論争の的となる問題です。先駆的な一連の研究で、マイケル・シャドレン、ビル・ニュースームとその共同研究者は、アカゲザルの外側頭頂間溝のニューロンが、拡散プロセスを実装していると期待されるのと非常によく似た挙動を示すことを観察しました(Shadlen and Newsome 2001)。これらの研究者は、動く刺激をサルに提示し、サルが動きが左か右かを指示しなければならない確率的運動弁別タスクを使用しました。実験者は、単一の試行における運動量(「証拠」)を制御できました。彼らは、外側頭頂間溝ニューロンが、応答野への眼球運動につながる選択肢では平均発火率が上昇し、応答野外への選択肢では下降することを発見しました。サッカード応答につながる前にニューロンの活動が上昇するレベルは固定されているように見え、拡散プロセスの境界を反映していました。さらに、簡単な試行では上昇の傾きが急であり、モデルのドリフト率を反映していました。それ以来、他の皮質および皮質下領域でも拡散プロセスの可能な相関関係が示されていることが発見されています。しかし、証拠の蓄積が実際の神経回路でどのように実装されているかはまだ議論されています。この問題は、第3章で記述されているような、大きな理論的進歩につながっています。
2.3 強化学習モデル²
機械学習における強化学習は、主に多段階(逐次的)意思決定問題における学習された最適制御の研究に関わります。この主題に関する古典的な研究のほとんどは、**マルコフ決定過程(MDPs)**として知られる種類のタスクに関係しています。MDPsは、迷路のナビゲーションやテトリスのようなゲーム(図2.3)などの多段階意思決定タスクの形式的なモデルです。強化学習の目標は通常、試行錯誤によって最適な選択を行うことを学習することです。
形式的に、MDPsは離散状態 s、行動 a、そして数値報酬 r の観点から表現されます。非形式的には、状態はタスクにおける状況(例:空間的迷路内の場所)のようなものであり、行動は行動上の選択(左に曲がるか右に曲がるか)のようなものであり、報酬は特定の状態(例:空腹であれば特定の場所で得られる食物の高い価値、またはお金)で得られる効用の尺度です。
MDPは、エージェントが環境のある状態 s を観察し、ある報酬 r を受け取り、ある行動 a を選択する一連の離散時間ステップから構成されます。エージェントの目標は、期待される累積的な将来の報酬を最大化するように、各ステップで行動を選択することです。将来の報酬は通常、それがどれだけ将来に受け取られるかによってペナルティが課せられます(近い将来に得られる報酬は遠い将来の同じ報酬よりも魅力的であるという直感的な考えを説明するため)。この遅延割引は通常、減衰因子 γ<1 を適用することによって実装されます。期待される累積的な将来の報酬は、その後の報酬の合計 rt+γrt+1+γ2rt+2+… として定義されます。したがって、目標は、行動の即時的な報酬を最大化するのではなく、すべての将来のタイムステップにわたって合計された累積報酬(別名「リターン」)を最大化することです。各行動は現在の報酬に影響を与えるだけでなく、次の状態に影響を与えることによって、その後の報酬のための舞台も設定します。結果として、最適に選択することは非常に複雑になる可能性があります。これらの問題をそれでも扱いやすくしているのは、MDPsの特性であるマルコフ条件付き独立性特性です。任意のタイムステップ t において、すべての将来の状態と報酬は現在の状態と行動にのみ依存します。これは、現在の状態と行動を条件とすると、すべての将来のイベントはすべての先行イベントとは独立していることを意味します。
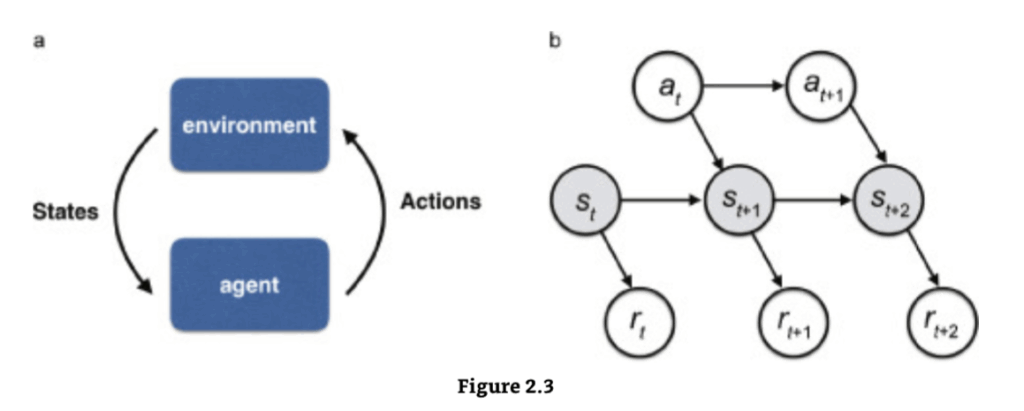
マルコフ決定問題
(a) 設定: エージェントは、行動を選択することで環境と相互作用し、その行動が現在の状態に影響を与えます。(b) 各タイムステップにおいて、エージェントはある状態 s におり、その状態で利用可能な任意のアクション a を選択できます。これにより、新しい状態に移動し、意思決定者に対応する報酬 r が与えられます。
このような問題を解決するために、各状態の「価値」を計算できます。状態価値は将来の期待報酬の合計として記述でき、マルコフ特性のおかげで、以下の再帰的な数学的表現を持ちます。
V(s)=E[rt+γrt+1+γ2rt+2+…∣st=s]
これは、現在の状態 s から得られる将来の割引報酬の期待値を示しています。より再帰的に書くと、以下のようになります。
V(s)=E[rt+1+γV(st+1)∣st=s,at=a] (2.9)
この式は、ある状態 s の価値が、その状態から行動 a を選択した結果として得られる即時報酬 rt+1 と、その後の新しい状態 st+1 の価値を割引率 γ で割引いたものの期待値の合計であることを示しています。
V(s)=E[rt+1+γV(st+1)∣st=s,at=a] (2.9)
この方程式(2.9)は、いわゆるベルマン方程式の一種であり、その様々な形式がほとんどの古典的な強化学習アルゴリズムの基礎となっています。ここで、これは状態 s における期待される将来の報酬が、現在の報酬と、残りのすべての報酬(+γrt+1+γ2rt+2+…)を表す第二項の合計によって与えられることを意味しています。この洞察は、この合計自体が、後続の状態の確率に従って平均化された、その後の状態 st+1 の価値 V にすぎないという点です。
環境内のすべての状態の価値を学習できれば(後述)、最も有望な状態へと向かうように行動を選択できます。エージェントは価値関数を使用して、各ステップでどの状態を選択するかを決定し、最も高い価値を持つステップを取ります。これは価値ベースの強化学習と呼ばれます。
一般的な代替手段として、方策ベースの強化学習というものがあります。これは、各状態 s で任意のアクション a をとる価値を直接計算する方法です。これは状態-行動価値関数 Q(s,a) と呼ばれ、私たちが最適化したい量です。この方程式は以前と同じ形式をとります。
Q(s,a)=E[rt+1+γmaxa′Q(st+1,a′)∣st=s,at=a] (2.10)
関数 π(s) は方策と呼ばれ、エージェントが与えられた状態においてどの行動を実行するかを選択する方法を示します。これは現在の環境状態を入力として受け取り、行動を返します。それは決定論的であることも確率論的であることもあります。
2.3.1 V または Q 値の学習
V 値をうまく推定できれば、最も高い価値を持つ状態へ移動するステップをとるだけで、最適な行動を選択できます。同様に、Q 価値関数の推定値があれば、候補となる行動間で Q 値を比較するだけで、最適な行動を選択できます。多くの強化学習アルゴリズムは、この基本的な論理のバリエーションに基づいています。
しかし、これらの価値はどのように学習するのでしょうか?方程式(2.9)に基づいた強化学習には、主に2つの主要なアルゴリズムクラスがあります。これらのクラスは、その方程式の等号の左側または右側のいずれかに焦点を当てています(Gershman and Daw 2017)。
最初の方法(方程式 [2.9] の右側に焦点を当てる)は、モデルベース強化学習として知られています。これは、確率的な内部モデル、つまり1ステップ報酬および状態遷移分布 P(rt∣st) と P(st+1∣st,at) の学習に依存するためです。これらの遷移は即時的なイベント、つまりどの報酬や状態が他の状態に直接続くかのみに関係するため、基本的には数えることによって局所的な経験から容易に学習できます。これらの確率が与えられれば、方程式(2.9)の右側を繰り返し展開して、任意の状態と可能な行動に対する状態-行動価値を計算することが可能です。価値反復などのこのためのアルゴリズムは、基本的にシミュレーションによって機能します。開始状態と行動に続く可能な状態のシーケンスをリストアップし、これらのシーケンスに沿って期待される報酬を合計し、学習されたモデルを使用してそれらの確率を追跡します。モデルベース学習の主な利点はその単純さにあります。しかし、この単純さは計算上の複雑さという代償を伴います。なぜなら、状態-行動価値の生成は、多くの分岐する可能な経路にわたる広範な計算に依存するからです。
2番目のアルゴリズムクラスはモデルフリー強化学習と呼ばれます。これらのアルゴリズムは、内部モデル(遷移と報酬の確率)を学習することを避けます。代わりに、経験と環境のサンプリングから直接、状態-行動価値のテーブル Q(方程式 [2.9] の左側)を学習します。
このようなアルゴリズム、特に時間差学習アルゴリズム(Temporal-Difference learning algorithms)(Sutton 1988)の発見は、機械学習における大きな進歩であり、現代の応用における基盤を提供し続けています。
手短に言えば、これらのアルゴリズムは、経験された状態、行動、および報酬を使用して方程式(2.9)の右側を近似し、これらを平均して長期的な報酬予測のテーブルを更新します。より正確には、多くのアルゴリズムは報酬予測誤差 δt と呼ばれる量に基づいています。この量は、価値 V(st)(予測された報酬)と実際の報酬 rt+1 および1タイムステップ後に計算された予測 V(st+1) の合計との比較に対応します。
δt=rt+1+γV(st+1)−V(st) (2.11)
Q 値を学習している場合も表現は同様です: δt=rt+1+γQ(st+1,at+1)−Q(st,at)。価値関数がうまく推定されている場合、この差は平均してゼロになるはずです。しかし、価値が間違っている場合、方程式の両側に不一致が生じます。その場合、格納された価値は不一致を減らすために繰り返し更新されます。
V(st)new=V(st)old+αδt=V(st)old+α(rt+1+γV(st+1)−V(st)) (2.12)
ここで、α は 0 から 1 の間の学習率です。これは時間差アルゴリズムとして知られています。
モデルフリーモデルにおける意思決定は、長期的な価値が事前に計算されており、最適な行動を見つけるために比較するだけでよいため、モデルベースアルゴリズムを使用するよりもはるかに単純です。しかし、この計算上の単純さは、柔軟性の欠如と学習効率の低さという代償を伴います。
第10章のボックス10.1も、一般的に使用される強化学習モデルの紹介、特にQ学習とアクター・クリティックモデルの比較について参照できます。
2.3.2 脳における強化学習
理論と神経科学を結びつける最も有名な成功例の1つは、サルが報酬学習タスクに従事しているときに、中脳のドーパミンニューロンの発火が方程式(2.11)の報酬予測誤差に類似しているという観察でした(Montague, Dayan, and Sejnowski 1996)。これは、脳が強化学習のためにこの信号を使用していることを示唆しています。この信号の試行ごとの変動はモデルを非常に正確に追跡し、げっ歯類では生理学とボルタンメトリーの両方を使用して測定することもできます。同様の信号は、ヒトの腹側線条体(ドーパミンニューロンの重要なターゲット)でもfMRIを使用して測定できます。多くの研究者は、ドーパミンがそのターゲット、例えば線条体における可塑性を変調することによって、行動に関する学習を促進すると考えています。ドーパミン作動性反応の誘発と抑制は、誤差駆動型学習を単離するために特別に設計されたタスクにおける学習を変調することが示されています。
ドーパミンと予測誤差の間の関連性は、精神疾患や依存症などの不適応行動を理解する上で重要な意味を持ちます。例えば、第9章で見るように、乱用薬物は例外なくドーパミンニューロンに作用します。これは、薬物乱用と依存症のいくつかの側面が、薬物が予測誤差信号を妨害することによって強化学習プロセスを乗っ取り、薬物につながる行動にますます高い価値を与えるという観点から理解できることを示唆しています。
第10章のボックス10.1と10.2は、トーニックおよびフェイジック線条体ドーパミンが行動選択と学習にどのように貢献するかについてさらに詳細を述べています。
2.3.3 モデルベースシステムとモデルフリーシステムのエビデンス
脳がモデルベース学習またはモデルフリー学習のどちらを、またはいつ使用しているかをどのように評価できるでしょうか?モデルフリーアルゴリズムとモデルベースアルゴリズムはどちらも最終的には最適な価値予測に収束しますが(様々な技術的仮定の下で)、解に接近する試行ごとのダイナミクスが異なります。一方または他方のモデルの証拠は、モデルフリー学習者を打ち負かすように順序付けられた段階的な経験のシーケンスを使用する実験タスクで示すことができます。
例えば、潜在学習または「感覚事前条件付け」タスクでは、動物はまず報酬のない環境に事前にさらされます(例:迷路を探索することによって)。その後、特定の場所に報酬が導入されます。モデルベース学習者にとって、この経験は、まず遷移関数 P(st+1∣st,at)、つまり迷路の地図を学習し、その後、報酬関数 P(r∣s) を学習し、それらをモデルに組み込む結果となります。しかし、モデルフリー学習者にとっては、事前露出段階は有用な何も教えてくれません(Q 値がどこでもゼロであることだけ)。彼らは迷路の地図の表現(状態遷移分布)を学習しません。このため、報酬が導入されると、ナビゲーションタスクを一から再学習する必要があります。
動物の行動におけるモデルフリー学習の証拠はいくつかあります。理論が予測するように、特定の状況下では、動物は偶発性と報酬に関する情報を、両方の種類の情報が別々に学習されている場合に統合できません。例えば、食物を得るためのレバー押しを過剰に訓練した後、げっ歯類は満腹になった後でもレバーを押し続けます。これは満腹が結果の価値の低下に対応しているにもかかわらずです。しかし、訓練が不十分な動物はうまく適応できます。一般に、動物が報酬価値(例:結果の価値低下)やタスクの偶発性の変化後に意思決定をどのように調整するかを調べる実験は、彼らの行動がモデルフリー強化学習だけでは完全に説明できないことを示しています。
心理学では、これら2種類の行動(それぞれ統合不可能と統合可能)は、**習慣行動(habitual behaviors)と目標指向行動(goal-directed behaviors)**として知られています。モデルフリー学習の予測とドーパミンの予測誤差理論は、習慣行動によく一致しますが、目標指向行動や、生物が経験を統合する能力を説明するには不十分です。モデルベース学習はモデルフリーシステムと並行して動作し、両システムが行動出力を制御するために競合していると考えられています(Daw, Niv, and Dayan 2005)。脳がこれらのシステムのどちらが特定の瞬間に行動を制御するかをどのように決定するかについては、ほとんど知られていません。モデルベースとモデルフリーの価値間の裁定を管理するために様々なモデルが提案されています。例えば、それらの相対的な確実性(学習の程度や計算の非効率性に依存して変化する。Daw et al. 2005)や、モデルベースの計算を実行するのにかかる時間の機会費用(Keramati, Dezfouli, and Piray 2011; Pezzulo, Rigoli, and Chersi 2013)などがあります。例えば、Lee, Shimojo, and O’Doherty (2014) は、モデルベースシステムとモデルフリーシステムによる行動制御の程度を、それぞれの予測の信頼性の関数として割り当てる裁定メカニズムを提案しました(図2.4; 本書第5.2.2節)。

二段階意思決定課題
(a) 各試行において、2つの刺激から1つを選択すると、固定された確率(遷移)でステージ2の2つの刺激のペアのいずれかにつながります。4つの第二段階刺激のそれぞれは、確率的な結果(金銭的報酬)と関連付けられています。これらの確率は試行ごとにゆっくりと独立して変化します。(b) モデルベース戦略とモデルフリー戦略は、第二段階後に得られた結果がその後の第一段階の選択に与える影響について異なる予測を立てます。したがって、これらは異なる選択パターンを予測します。
- モデルフリーシステムでは、報酬を得ると、遷移の種類がまれなものであったか一般的なものであったかにかかわらず、次の試行で同じ刺激を選択する可能性が高まります(上段)。
- モデルベースシステムでは、反対に、次の試行における刺激の選択は遷移の種類を統合します(下段)。
Worbe et al. (2015c) より許可を得て転載。
2.3.4 精神医学への示唆
モデルベース学習とモデルフリー学習の区別は、精神医学にとって特に重要であると思われます。特に、依存症や強迫性障害は、モデルベースの意思決定からモデルフリーの意思決定への移行を伴う可能性があり、これが患者の柔軟性のない行動を説明すると提案されています。
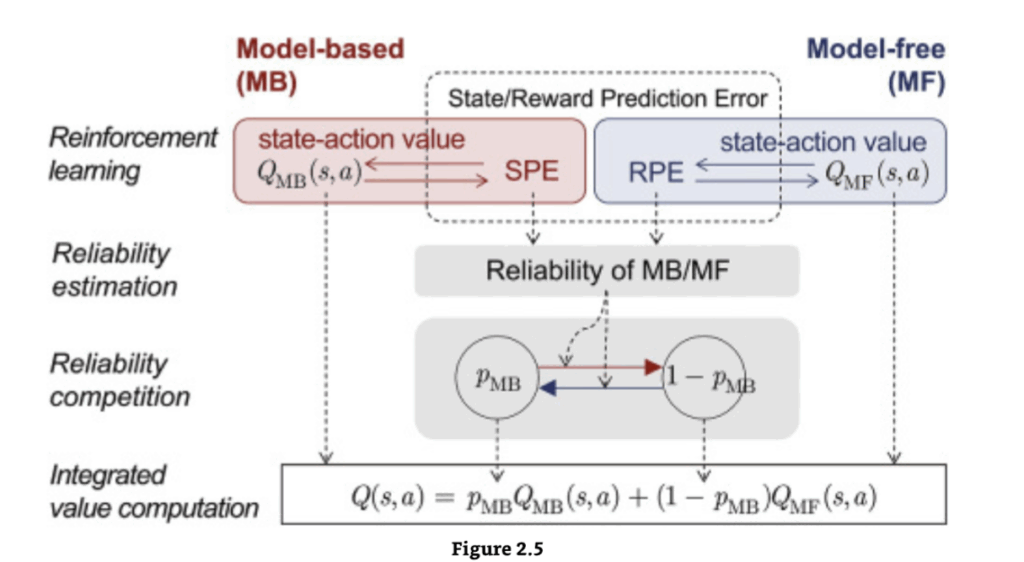
モデルベース学習戦略とモデルフリー学習戦略の間の可能な裁定の例
蓄積された神経科学的証拠は、行動選択を導く2つの異なるシステム、すなわち熟考的な「モデルベース」システムと反射的な「モデルフリー」システムの存在を裏付けています。しかし、脳がこれらのシステムのどちらが特定の時点で行動を制御するかをどのように決定するのかについては、ほとんど知られていません。1
Lee et al. (2014) は、モデルベースシステムとモデルフリーシステムによる行動制御の程度を、それぞれの予測の信頼性の関数として割り当てる裁定メカニズムを提案しています。信頼性は、モデルベース学習システムにおける状態予測誤差(SPE)と、モデルフリー学習システムにおける報酬予測誤差(RPE)に基づいて計算されます。計算された信頼性は、2状態遷移モデルの遷移率として機能し、各状態はそれぞれモデルベース学習戦略を選択する確率 (PMB) とモデルフリー学習戦略を選択する確率 (1−PMB) を表します。実際の選択行動を制御する状態-行動価値は、2つの強化学習システムからの価値の加重平均によって与えられます。Lee et al. (2014) より許可を得て転載。
Daw et al. (2011) は、個人内の2種類の学習間のトレードオフを測定するためのタスク(図2.5)を設計しました。このタスクはその後広範囲に検討され、目標指向制御の欠陥と強迫行動との関連性を示すいくつかの証拠が報告されています(Gillan et al. 2016)。
より一般的に言えば、学習の欠陥は精神疾患で観察される問題の核心にある可能性があります。学習と意思決定は密接に絡み合ったプロセスです。学習メカニズムが損なわれると、不適応な意思決定がなされ、それが今度は何を学習するかを左右することになります。
精神疾患の患者が「間違った」世界の内部モデルで機能しているという考えは、次に議論するベイジアンアプローチの中心的な考えでもあります。
2.4 ベイジアンモデルと予測符号化
2.4.1 不確実性とベイジアンアプローチ
ベイジアンアプローチは、私たちが不確実な世界に生きているという考えに焦点を当てています。私たちの環境はしばしば曖昧でノイズが多く、感覚受容器には限界があります。多くの場合、複数の解釈が可能です。このような文脈において、私たちの脳ができる最善のことは、世界で何が起こっているのか、そして最善の行動は何であるかを推測することです。
脳を「推測する機械」と捉えるこの考えは、近年、機械学習や統計学のアイデアを取り入れて形式化されています。脳は、世界に何が存在し、どのような行動をとるべきかについて、常に仮説(「信念」)を形成し、現在の証拠と事前の知識に基づいてそれらの仮説を評価することによって機能すると提案されています。これらの仮説は、条件付き確率、すなわち P(仮説∣データ) として数学的に記述できます。これは、データが与えられた場合の仮説の確率であり、「データ」は私たちの感覚で利用できる信号を表します。統計学者は、これらの確率を計算する最良の方法は、トーマス・ベイズ(1701-1761)にちなんで名付けられたベイズの定理を使用することを示しています。
P(仮説∣データ)=P(データ)P(データ∣仮説)P(仮説) (2.13)
ベイズの定理は統計学において根本的に重要です。ベイズの定理を用いて信念を更新することをベイズ推論と呼びます。
例えば、今日雨が降るかどうかを推測しようとしているとしましょう。利用可能なデータは、窓から見える黒い雲かもしれません。ベイズの定理は、私たちが信念、すなわち事後確率と呼ばれる P(仮説∣データ) を、他の2つの確率を掛けることによって更新できると述べています。
- P(データ∣仮説): 尤度と呼ばれ、「実際に雨が降ることを知っているとして、雲が今のように見える可能性はどれくらいか?」といった、仮説が与えられた場合のデータの確率に関する私たちの知識を表します。
- P(仮説): 事前確率と呼ばれ、新しい情報を収集する前に仮説について持っている知識を表します。この例では、雲の形とは無関係に、1日で雨が降る確率であり、これはエディンバラに住んでいるかロサンゼルスに住んでいるかによって大きく異なる数値になります。

