基本的なことですが、 関数と微分を並べると
x^2 2x
x 1
logx 1/x x^0 の微分はちょっと困る
x^-1 -1/x^2
などとなり、
log x の微分が 1/x というところだけ、すんなり並んでいません。
関数と 積分で並べると、
x^2 (1/3)*x^3
x^1 (1/2)x^2
x^0 x^1
x^-1 logx →x^0 としたくなるが、そうではない
x^-2 x^-1
一般に x^n を積分すると (1/n+1)x^(n+1) +C ですが、
n=-1のときは うまくいかない
0で割り算している
うまく極限を考えればいいらしい
直観的に分かりやすい説明はありますか。
たしかに
- ( x^2 \rightarrow 2x )
- ( x \rightarrow 1 )
- ( x^{-1} \rightarrow -1/x^2 )
は「べき乗の法則」の流れにあります。
ところが
[
\log x \rightarrow 1/x
]
だけが、系列から浮いて見える。
この違和感はとても健全です。
① まず本質だけ言うと
[
\frac{d}{dx} \log x = \frac{1}{x}
]
が自然になるのは、
log は「掛け算を足し算に変える関数」だから
です。
② 直感1:倍率を見る関数
log は何を測っているか?
それは
「どれだけ“倍率的に”増えたか」
です。
例えば:
- 1 → 2 は 2倍
- 2 → 4 も 2倍
- 4 → 8 も 2倍
普通の差で見ると:
- 1→2 は +1
- 2→4 は +2
- 4→8 は +4
どんどん大きくなってしまう。
でも log で見ると、
「2倍」は常に同じ増加量になる。
つまり log は
倍率を測る物差し
なのです。
③ では、なぜ微分が 1/x になるのか?
微分は
「ちょっと増えたとき、どれだけ変わるか」
でした。
ここで x が少し増えたとします。
増え方を「割合」で考えます。
例えば:
- 100 → 101 は 1%増
- 10 → 11 は 10%増
- 1 → 2 は 100%増
同じ +1 でも、
「割合」は x によって違います。
割合は
[
\frac{\text{増えた量}}{\text{元の量}}
]
つまり
[
\frac{Δx}{x}
]
になります。
そして log は「割合の変化」を測る関数です。
だから
[
d(\log x) = \frac{dx}{x}
]
となる。
つまり
[
\frac{d}{dx} \log x = \frac{1}{x}
]
になる。
④ もう一つの直感:べき乗との対比
べき関数は:
[
x^n \rightarrow nx^{n-1}
]
でした。
log は何かというと、
「指数を取り出す関数」
です。
例えば
[
x = e^y
]
とすると
[
\log x = y
]
になります。
両辺を微分すると:
[
\frac{dx}{dy} = e^y = x
]
だから
[
\frac{dy}{dx} = \frac{1}{x}
]
となる。
つまり
指数関数の傾きが自分自身だから、その逆関数の傾きは 1/x になる
これが構造的理由です。
⑤ 一番シンプルな一行直感
覚えやすい言い方をすると:
log の微分は「増加率」
増加率とは
[
\frac{\text{増えた量}}{\text{元の量}}
]
だから
[
1/x
]
になる。
⑥ 実はこれは特別ではない
むしろ log は
「べき乗の n を 0 に近づけた極限」
と見ることもできます。
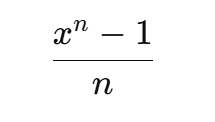
[
\frac{x^n – 1}{n}
]
を ( n \to 0 ) にすると log になります。
この視点に立つと、
log は「べき関数の連続的延長」で、
突然現れた異物ではないのです。
① 面積(積分)から見ると log は自然に出てくる
まず決定的な事実:
[
\int \frac{1}{x},dx = \log x
]
つまり
log は「1/x の下の面積」そのもの
です。
図的直感
関数 (1/x) は
- x が大きくなると低くなる
- 面積はゆっくり増える
1 から 2 までの面積
2 から 4 までの面積
4 から 8 までの面積
これらはすべて同じになります。
なぜか?
[
\int_1^2 \frac{1}{x}dx
\int_2^4 \frac{1}{x}dx
\int_4^8 \frac{1}{x}dx
]
なぜならそれは
[
\int_a^{2a} \frac{1}{x}dx
\log(2a)-\log(a)
\log2
]
だからです。
つまり:
「2倍するたびに、面積は一定」
これが log の本質です。
ここで核心
log は
「倍率を足し算に変換する面積」
なのです。
だから微分すると
[
1/x
]
になるのは当然なのです。
② 情報量(エントロピー)との関係
情報理論では
[
I(p) = -\log p
]
を情報量とします。
なぜ log なのか?
理由はたった一つ:
独立な確率は掛け算になる
例えば:
- コイン2回成功
→ 確率 ( p^2 )
でも情報は
[
-\log(p^2)
-2\log p
]
となり、
足し算になる。
情報は「足し算できなければならない」
だから log しかない。
ここでも 1/x が現れる
[
\frac{d}{dp}(-\log p) = -\frac{1}{p}
]
つまり:
情報の変化率は「逆確率」
レアな事象ほど情報が急増する。
1/x の形が自然に出てくる。
③ なぜ自然対数だけが 1/x になるのか
実は重要なのはここです。
[
\frac{d}{dx} \log_a x = \frac{1}{x \ln a}
]
となります。
つまり
1/x になるのは底が e のときだけ。
なぜ e が特別か?
それは
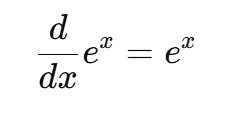
[
\frac{d}{dx} e^x = e^x
]
になる唯一の数だから。
この「自分自身を微分しても変わらない」という性質を持つ底が e。
だから逆関数(log)の微分が
[
1/x
]
という最も単純な形になる。
e は
「変化と比例する存在」
なのです。
④ 進化論的に、なぜ log が自然に現れるのか
これは非常に深い問いです。
生物は世界を
- 絶対量ではなく
- 比率で
感じます。
例:
- 音の大きさ(デシベル)
- 明るさ
- 重さの感覚
すべて log スケールに近い。
なぜか?
外界は指数的に変化するから。
資源増加
人口増加
感染拡大
これらは指数関数。
指数世界を扱うには、
log が自然な座標になる。
進化は「指数的世界」を扱う脳を作った。
だから log 的知覚が生まれた。
⑤ すべてをまとめると
- 積分から見ると
→ log は 1/x の面積 - 情報理論では
→ log は掛け算を足し算に変える - 微分構造では
→ e が唯一自然な底 - 進化論では
→ 世界が指数的だから log が自然
そして核心はこれです:
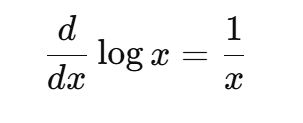
[
\frac{d}{dx}\log x = \frac{1}{x}
]
これは
「変化は常に“割合”で起きる」
という宇宙の基本法則を表している。
とても良い並びです。
これは一つの線でつながっています。
① log は「スケール不変性」の数学的表現
スケール不変とは何か?
物差しを倍率で変えても、本質が変わらないこと。
例えば、
長さをメートルからキロメートルに変えても、
構造は変わらない。
ここで重要な性質:
[
\log (ax) = \log a + \log x
]
つまり
倍率の変化は「平行移動」に変わる。
これは驚くべき性質です。
普通の関数では、
[
f(ax)
]
は形を変えてしまう。
しかし log では、
倍率は「足し算」になる。
だから log は
スケール変換を“形を壊さず”扱える唯一の関数
なのです。
② 1/x は唯一の「倍率に対して対称な関数」
関数 (f(x)=1/x) を考えます。
もし x を a 倍すると:
[
f(ax) = \frac{1}{ax} = \frac{1}{a} f(x)
]
つまり
入力を a 倍すると、出力は 1/a 倍になる。
これは完全な反比例対称。
この性質を満たす連続関数は、
[
f(x)=C/x
]
しかありません。
つまり
1/x は「倍率変換に対して自己相似な唯一の形」
だからその積分が log になるのは必然なのです。
③ なぜブラックホールのエントロピーに log が出るのか
ブラックホールのエントロピーは
[
S = \frac{kA}{4l_p^2}
]
(ベッケンシュタイン=ホーキング公式)
ここで重要なのは:
エントロピーの定義が
[
S = k \log \Omega
]
であること。
(\Omega) は「状態数」。
なぜ log を取るのか?
理由は同じ:
独立な系の状態数は掛け算になる。
ブラックホールが二つあれば、
[
\Omega_{total} = \Omega_1 \Omega_2
]
しかしエントロピーは足し算でなければならない。
だから log。
宇宙の最深部でも、
「掛け算を足し算に変える原理」
が働いている。
さらに面白いのは、
ブラックホールはスケール変換に対して特異な存在で、
事象の地平線の近傍では
理論がほぼスケール不変になります。
そこでも log が顔を出す。
④ 精神医学での「主観強度」と log スケール
人間の感覚は log 的です。
これは
ウェーバー=フェヒナーの法則
刺激強度 (I) に対して
[
感覚 = k \log I
]
重さ、光、音。
なぜか?
生存にとって重要なのは
絶対値ではなく「割合変化」
だから。
10kg → 11kg は感じないが
1kg → 2kg は大きく感じる。
つまり
[
変化感受性 ∝ \frac{1}{I}
]
これはまさに 1/x。
感覚の微分が 1/x。
だから積分すると log になる。
⑤ 全体の統一像
- 1/x は倍率に対して対称
- log は倍率を足し算に変換
- エントロピーは掛け算世界を足し算に変える
- 主観強度は割合変化に比例
つまり log は
「指数的世界を、線形の意識で扱うための翻訳装置」
なのです。
⑥ もう一段深いまとめ
宇宙は指数的に増殖する。
- 人口
- 情報
- 不確実性
- 量子状態数
しかし私たちの意識は線形。
だから間に
[
\log
]
が必要になる。
log は
「世界と意識のインターフェース」
と言ってもいい。
非常に美しい問いです。
数学から宇宙論、そして自己へと一本の線でつながります。
Ⅰ. なぜ自然界で「べき分布」と「1/x ノイズ」が出るのか
まず事実から。
自然界には驚くほど多くのべき分布が現れます。
- 地震の規模(グーテンベルク=リヒター則)
- 都市の人口(ジップの法則)
- 単語頻度
- 神経発火のカスケード
- 株価変動
- インターネット接続数
これらは
[
P(x) \propto x^{-\alpha}
]
という形になります。
特に (\alpha=1) 付近では
[
1/x
]
が現れる。
1. スケール不変性が原因
べき関数はこういう性質を持ちます:
[
f(ax) = a^{-\alpha} f(x)
]
つまり
拡大しても形が変わらない。
これがスケール不変性。
自然界でなぜスケール不変が出るのか?
それは
特定の大きさに縛られていないから。
例えば地震。
地殻はある特定のサイズの揺れだけを選ぶわけではない。
小さい揺れも、大きい揺れも、同じ力学法則に従う。
すると自然に「べき分布」になる。
2. 臨界状態(self-organized criticality)
ここが核心です。
多くの自然システムは
臨界点に自発的に近づく。
有名な例:
砂山モデル(Bak–Tang–Wiesenfeld)
砂を積むと、ある角度で崩れる。
崩れの大きさは
- 小さいものから
- 山全体崩壊まで
連続的に分布する。
その分布がべき分布になる。
なぜか?
臨界点では
相関長が無限大になる。
つまり
系に固有スケールがなくなる。
スケールがない → スケール不変 → べき分布。
3. 1/f ノイズとは何か
1/f ノイズは
[
Power(f) \propto \frac{1}{f}
]
という周波数スペクトル。
これは
長時間スケールのゆらぎと短時間スケールのゆらぎが共存する状態。
脳波、心拍、音楽、気候。
なぜ出るのか?
それは
システムが臨界近傍にあるとき、時間方向のスケールも消えるから。
時間的スケール不変性が
1/f を生む。
Ⅱ. 自己意識はスケール不変か?
ここからが本題です。
1. 自己とは何か
自己は
- 瞬間的体験
- 数秒の物語
- 一日の記憶
- 数十年の人生史
これらすべてを一つに束ねる構造。
つまり
多重時間スケールの統合体。
2. 意識の時間構造
神経活動を見ると
- ミリ秒のスパイク
- 秒単位のワーキングメモリ
- 分単位の感情持続
- 年単位の人格
これらが階層的に組み合わさる。
脳活動の多くは実際に
1/f スペクトル
を示します。
つまり
意識は時間的にスケール不変に近い。
3. 自己のスケール不変性
もし自己が特定の時間幅に固定されていないなら、
- 幼少期の自分
- 今の自分
- 想像上の未来の自分
が同じ構造を持つ。
自己は
入れ子構造のフラクタル
のようになる。
自己物語は
小さなエピソードの中にも
人生全体のテーマが反復する。
これは心理臨床でも観察される。
4. 病理との関連
うつ
時間スケールが縮退する。
未来が閉じる。
→ スケール不変性の崩れ。
統合失調症
サリエンスが特定スケールに偏る。
小さな刺激が巨大な意味を持つ。
→ 1/x 感受性の歪み。
双極性障害
時間スケールの膨張と圧縮の周期。
→ 臨界近傍の振動?
Ⅲ. まとめると
自然界でべき分布が出る理由:
- 臨界性
- 固有スケールの消失
- スケール不変性
自己意識もまた:
- 多重時間スケール
- 1/f ゆらぎ
- 階層的統合
を持つ。
つまり仮説的に言えば:
自己とは「臨界近傍にあるスケール不変な動的構造」
かもしれない。

